摘要(yao):通過數值模(mo)拟的方法孔(kǒng)闆厚度對槽(cáo)式孔闆流量(liang)計
内部流場(chǎng)及流出系數(shu)的影響。在雷(léi)諾數從3×104到9×104的(de)範圍内,對💛不(bu)同的直徑比(bi)(β=0.4,0.5,0.6)和不同孔闆(pan)厚度(E=0.05D,0.12D,0.18D)的槽式(shi)孔闆流量計(jì)進行了研㊙️究(jiū)。結果表明:與(yu)标準孔闆流(liu)量計相比,槽(cáo)式孔闆流量(liang)計對孔🎯闆厚(hòu)度的變化更(gèng)敏🔞感;同時,β越(yuè)大,槽式孔闆(pǎn)流量計的流(liú)出系數變化(huà)越明顯。在本(běn)項目的研究(jiu)範圍内,當孔(kǒng)闆厚度由0.05D增(zēng)加🈚到0.12D時,β爲0.4,0.5和(he)0.6的🍉槽式孔闆(pǎn)流量計⭐的流(liú)出系數分别(bie)增大了4.31%~6.04%,4.92%~6.66%和5.87%~7.57%。當(dang)孔闆厚度由(you)0.12D繼續增大到(dao)0.18D時,β爲0.4的流量(liàng)計🈲流出系數(shù)基本不變,而(er)β爲0.5和0.6的流量(liang)計流出系數(shù)分别增大了(le)🙇♀️0~0.87%和0.33%~1.79%。
孔闆流量(liang)計
由于具有(yǒu)結構簡單、操(cao)作方便、技術(shù)成熟、性能穩(wen)定等優點,被(bei)廣泛應用于(yu)石油、天然氣(qi)和化工等行(hang)業。提高孔闆(pan)流量計的計(jì)量精度能夠(gòu)帶來巨大的(de)經濟效益🌏,因(yin)此在過去的(de)數十年裏研(yan)究人員對其(qi)進行了大量(liàng)的研究[1-4].。Morison等[[5]通(tong)過試驗研究(jiu)了,上遊速度(du)分布對孔闆(pǎn)流量計性能(néng)的影響,研究(jiu)發㊙️現,中心速(sù)率和直徑比(bǐ)越小,通過孔(kǒng)闆的壓降越(yue)大,進而導緻(zhi)流出系數降(jiang)🧡低。Nail6]公布了通(tōng)過☎️多普勒激(ji)㊙️光測速儀測(ce)量的不同直(zhí)徑比和雷諾(nuò)數下孔闆流(liu)量計的中心(xin)線軸向速度(dù)、壁面靜壓.壁(bì)⁉️面剪切應力(li)等試驗數據(ju)。Shaaban'7]通過數值模(mó)拟的方法對(duì)孔闆流量計(ji)的結構進行(háng)了👣優化,在孔(kǒng)闆下遊引進(jìn)一個環從而(er)減小了通過(guò)孔闆的🔞壓力(lì)損失。Shah等[8]通過(guò)CFD詳細研究了(le)孔闆附近速(su)度、壓力、湍動(dòng)能和湍動能(néng)耗散率的分(fèn)布,根據模拟(ni)結果提出了(le)一種在保留(liu)原有優點的(de)基礎.上更加(jiā)👨❤️👨正确的壓差(cha)測量方式。
流(liú)量計量對于(yu)石油和天然(ran)氣行業非常(chang)重要,每年由(you)☂️于孔闆流量(liàng)計的計量誤(wù)差而産生的(de)花費相當大(dà),因此,開發低(di)價格、精度高(gao)的新型流量(liàng)計具有巨大(da)的經濟價值(zhi)。一種槽式孔(kǒng)闆流量計,相(xiang)比于标準的(de)孔闆流量計(jì),這種流量計(jì)具有更小的(de)壓力損失和(he)更快的壓力(lì)恢複,同時對(dui)上遊的渦旋(xuán)具有更低⭐的(de)敏感度。在這(zhè)之後,很多學(xue)者對這種流(liú)量計展開了(le)更充分的研(yan)究❓。通過數值(zhi)計算研究了(le)不同幾何形(xing)狀槽孔的孔(kong)闆流量計的(de)性能,并用其(qi)數值模型對(duì)9種不同的濕(shi)氣流量🐇測量(liàng)經驗公式的(de)正确率進行(hang)了評估。比較(jiao)了幾種典型(xíng)的标準節流(liu)元件測量💁兩(liang)相流流量的(de)試驗關聯式(shi),并對槽式孔(kong)闆流量計測(cè)量兩相流流(liú)量時産生誤(wu)差的原因進(jin)行了分析,然(ran)後在大量試(shi)驗數據的基(jī)礎上💚,提出了(le)用槽式孔闆(pan)進行濕氣測(ce)量的試驗關(guan)聯式,這些關(guān)聯式在試驗(yan)參數範圍内(nei)更準确。
國際(jì)标準ISO5167中規定(dìng)的标準孔闆(pǎn)的厚度爲(0.02~0.05)D(D爲(wèi)管道内徑),而(er)在許🚶多工業(ye)應用中,管道(dao)内的壓力很(hěn)高,爲了保證(zhèng)足夠的機械(xie)強度,需要增(zeng)加孔闆的厚(hòu)度。對于槽式(shi)孔闆顯然🙇🏻也(yě)有同樣的需(xu)求,因此研究(jiu)孔闆厚度對(dui)槽式孔闆流(liú)量♍計性能的(de)影響具有一(yī)定的工程價(jià)值和經♌濟價(jia)值。通過數值(zhi)模拟的📱方法(fa)研究了孔闆(pǎn)厚度對槽式(shì)孔闆流量計(jì)内部流場及(ji)流出系數的(de)影響,并和标(biāo)✂️準孔闆進行(hang)對比。
1計量原(yuán)理
根據文獻(xian)[9],槽式孔闆流(liu)量計的工作(zuò)原理和标準(zhun)孔闆流量🔞計(jì)相同,不同之(zhi)處是标準孔(kǒng)闆隻在孔闆(pǎn)中心有一個(ge)開口,而槽式(shi)孔👅闆的流通(tong)面積由若幹(gan)圈在整個管(guǎn)道截面上均(jun)😘勻分布的相(xiàng)同的槽孔組(zu)成。當流體流(liu)過孔闆時⛱️由(yóu)于流道收縮(suō)會産生壓降(jiàng),根‼️據連續性(xing)方⛱️程和伯努(nu)利方程可以(yǐ)得到壓降和(hé)流體流量之(zhī)間存🏃🏻♂️在以下(xia)關系:

壓差ΔP通(tong)過孔闆上下(xià)遊的2個取壓(ya)口測量得到(dao),對于标準的(de)㊙️孔闆流量計(ji),最常見的取(qǔ)壓方式爲标(biao)準的法蘭💃🏻取(qǔ)壓。在其研究(jiu)中也使用了(le)這種取壓方(fang)式,因🈲此在本(běn)文中也選擇(zé)标準的法蘭(lán)取壓👅來測量(liang)壓差。
2數值方(fang)法
2.1幾何結構(gòu)
本文中所使(shǐ)用的标準孔(kǒng)闆和槽式孔(kǒng)闆的結構簡(jian)圖見圖1,其中(zhōng)d爲标準孔闆(pǎn)流量計節流(liu)孔直徑,d,爲槽(cáo)式孔☎️闆流量(liàng)計節流❤️孔直(zhí)🛀徑,x1爲孔闆中(zhong)心到内部孔(kǒng)邊界的🈲長度(du),x2爲中部孔邊(biān)界到外部孔(kong)邊界的長度(du)。
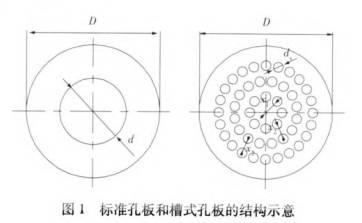
槽(cao)式孔闆具體(tǐ)的幾何參數(shu)見表1,孔闆上(shàng)下遊管道⛷️長(zhang)🌏度都是20D。
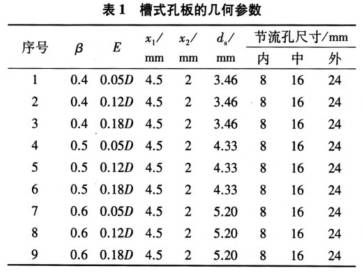
以空(kong)氣爲工作流(liu)體,在雷諾數(shu)3×104~9×104的條件下,對(duì)不同直🥵徑✏️比(bi)(β=0.4,0.5,0.6)和不同🈲孔闆(pan)厚度(E=0.05D,0.12D,0.18D)的9種不(bu)同幾何尺寸(cùn)的孔闆流量(liàng)計進行研究(jiū)。雷諾數Re定義(yì)爲:

式(3)中:空氣(qì)的動力黏度(dù)μ=1.845×10-5Pa.·s,密度ρ=1.177kg/m3,管道内(nèi)徑D=60mm。
2.2網格生成(cheng)
網格生成在(zài)數值模拟中(zhong)很重要,因爲(wei)它關系到數(shu)值♻️計算的穩(wen)定性、經濟性(xing)。在本文中,使(shǐ)用結構性和(he)非結構性網(wang)格來離散整(zhěng)個計算區域(yù),考慮到孔闆(pan)和管道壁面(mian)附近的速度(dù)梯度和壓力(lì)梯度較大,這(zhe)些地方使用(yong)尺寸更小的(de)網格😘。孔闆表(biao)面的網格如(rú)圖2所示。
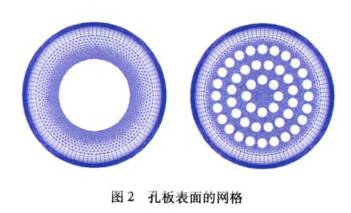
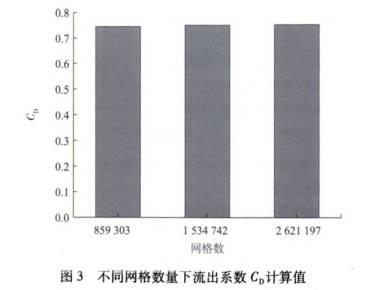
爲了證明數(shù)值模型的正(zhèng)确率,需要對(duì)模型進行網(wang)😘格獨立性🈲測(cè)試。分别用包(bāo)含859303個節點、1534742個(gè)節點和2621197個節(jie)☁️點的3種網格(ge)系統對一個(ge)基本算例(β=0.4,E=0.05D,Re=9000)進(jìn)行計算,計算(suan)🥵結果如圖3所(suo)示。
由圖3可見(jiàn):當網格節點(dian)總數達到1534742個(gè)時,再增加節(jie)點📐數目,流出(chu)系數Cp的計算(suan)結果也基本(běn)不再發生變(bian)化✨(變化率低(dī)🔴于0.25%)。因此,包含(hán)1534742個🔞節點的網(wǎng)格系統将用(yòng)于💋後面的計(jì)算。
2.3控制方程(chéng)
爲了簡化問(wèn)題,本文作如(rú)下假設:①管道(dao)水平放置,管(guǎn)壁水力光滑(huá),管内流動爲(wei)湍流,流體爲(wei)不可壓縮性(xìng)✌️流體;②流動爲(wèi)穩态流動;③忽(hu)略重力和黏(nian)性耗散;④流體(ti)爲常物性。基(jī)于上述假設(shè)建立了描述(shù)帶有孔闆流(liu)🚩量計的圓管(guan)内流體流動(dòng)的控制方程(cheng)。對于穩态、密(mì)度爲常數的(de)🔞不可壓縮性(xìng)流體,笛卡爾(er).坐标系中時(shi)均的Navier-Stokes方程可(ke)以🥰寫成如下(xia)形式。


2.4邊界條(tiáo)件和求解格(ge)式
進口速度(du)給定,出口壓(ya)力爲101325Pa。管道内(nei)壁和孔闆表(biao)面都是無💘滑(huá)移壁面,所有(you)壁面假設都(dōu)是完全光滑(huá)粗糙度爲零(ling)。通過給定湍(tuān)流強度[I=0.16(Re)-1/8]和水(shui)力直徑L,對湍(tuān)動量的值進(jin)行初始的估(gu)計。
在本研究(jiū)中,通過有限(xiàn)容積法來求(qiú)解控制方程(cheng)。采用二階迎(ying)風㊙️格式來離(li)散動能、湍動(dong)能和湍動能(neng)耗⭐散率,壓力(lì)插值♌使用标(biāo)準格式,使用(yòng)SIMPLE算法來處理(li)壓力和速度(dù)的耦合。當所(suo)有變量的歸(guī)一化殘差都(dou)小于10-5時認爲(wèi)求解收斂,然(ran)而,連續性方(fang)程的殘差可(ke)能💋在未達到(dao)10-5之前就會達(da)到-一個最低(dī)值。因此,質量(liàng)守🌐恒(進出口(kǒu)質量流量的(de)偏差低于0.1%)被(bèi)作爲收斂的(de)第二個判據(ju)。
3結果和讨論(lun)
3.1流場分布.
β=0.5,Re=60000時(shi)不同孔闆厚(hòu)度下槽式孔(kǒng)闆和标準孔(kǒng)闆附近(從孔(kǒng)⚽闆上遊1D到下(xia)遊5D)的速度雲(yun)圖和流線圖(tu)分别如圖5、圖(tú)6所示。
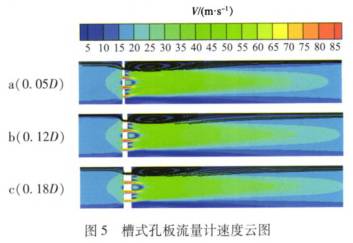
由圖(tu)5、圖6可見:對于(yu)标準孔闆流(liu)量計,所有流(liú)體隻能通🔞過(guo)✊孔🐕闆中心唯(wei)--的節流孔,當(dāng)流體流過孔(kǒng)闆時在下遊(yóu)形成了較🤩大(da)的射流和回(hui)流區,這兩者(zhě)之間是剪切(qiē)層🔴,在流體通(tong)過标準孔闆(pǎn)的過程中會(hui)消耗相對多(duo)的機械能從(cong)而産生相對(dui)大的壓降;而(er)槽式孔📧闆将(jiang)流通面積更(geng)加均勻地分(fèn)布在整個孔(kǒng)闆上,流.體通(tōng)過孔闆時形(xing)成了多個小(xiǎo)的射流和小(xiǎo)的回流區,同(tong)時可📱以看出(chu)槽式孔闆下(xia)遊速度明顯(xiǎn)小于标準孔(kong)闆,這一切都(dou)意♉味着流體(ti)通過槽式孔(kong)闆時的🏃♂️壓力(li)損失會更小(xiao)。
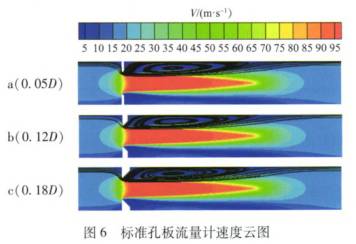
由圖6可見(jian):随着孔闆厚(hòu)度的增加,标(biāo)準孔闆附近(jin)的速度場和(hé)回流區大小(xiǎo)基本不變,即(jí)孔闆厚度對(dui)标準孔💛闆附(fù)近的流場基(jī)本沒有影響(xiang)。而對于槽式(shì)孔闆,由圖5可(kě)以發現,當孔(kǒng)闆厚度🤟從0.05D增(zeng)加到0.12D時,孔闆(pan)下遊速度在(zai)減小,這會☔減(jian)小速度㊙️梯度(du)和各☀️層間的(de)剪切應力進(jin)而減小流體(tǐ)流過孔闆時(shi)的💜機械能損(sǔn)失,而當孔闆(pǎn)厚度繼續增(zeng)加到0.18D時☀️,速度(dù)場則并無明(ming)顯變化。
與圖(tu)5、圖6所對應的(de)壁面靜壓分(fèn)布如圖7所示(shi),其中,X爲測🚩量(liang)點距孔闆上(shang)遊的距離(X的(de)正負值分别(bié)代表該🙇♀️點在(zài)孔闆上遊🏒和(he)孔㊙️闆下遊)。
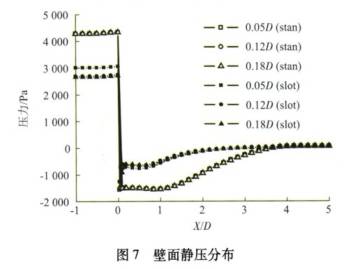
由(yóu)圖7可見:與标(biao)準孔闆相比(bi),流體流過槽(cao)式孔闆時的(de)壓🔆力損失更(gèng)小,這會使槽(cao)式孔闆有更(geng)大的流出系(xi)數;同時,相鄰(lín)射流間的相(xiàng)互幹涉加劇(ju)了流體的混(hùn)合,使孔闆下(xia)遊的壓力恢(huī)複得更快。此(ci)外,從圖7中🐪還(hai)可以看🔅出,孔(kǒng)闆厚度對标(biāo)準孔闆附近(jìn)㊙️的壓力分布(bù)幾乎沒有影(ying)響,這與圖6的(de)結論一緻。而(er)對于槽式💛孔(kong)闆,當孔闆厚(hòu)度由0.05D增加到(dào)0.12D時☔,流經孔闆(pan)的壓🌈降變🐕小(xiao),而當孔闆厚(hòu)度繼續增大(dà)到0.18D時,壓降繼(ji)續減小,但減(jian)小的幅度很(hěn)小。從圖5~圖7中(zhong)可以得出,相(xiang)比于标準孔(kǒng)闆流量計,槽(cao)式孔闆流量(liang)計對孔闆厚(hou)度的變化更(geng)敏感。
3.2流出系(xi)數
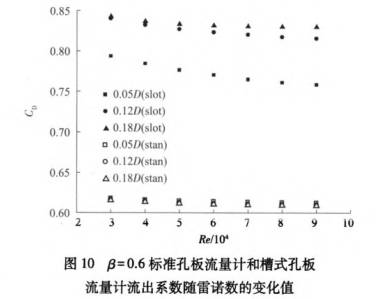
圖8、圖9、圖10所(suo)示分别爲β=0.4,0.5和(he)0.6時,孔闆厚度(dù)爲0.05D,0.12D和0.18D的标準(zhun)孔⭕闆流量計(ji)和槽式孔闆(pan)流量計流出(chu)系數随雷諾(nuò)數的變化。
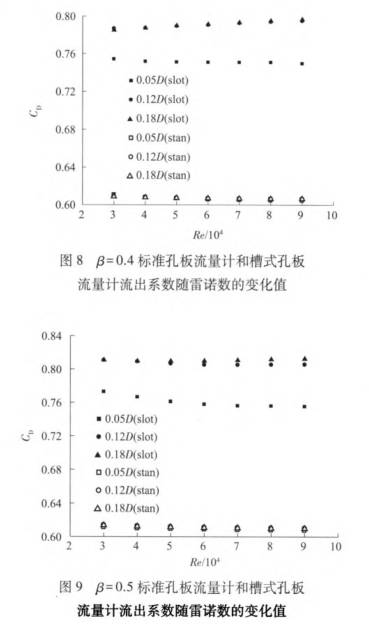
由(you)圖8~圖10可見:槽(cáo)式孔闆流量(liang)計的流出系(xì)數明顯高于(yú)标🈲準孔闆流(liú)量計,這是因(yīn)爲流體通過(guò)槽式孔闆👌時(shi)壓降更小。此(ci)外,随😄着孔闆(pan)厚度的變化(huà),标準孔闆流(liu)量計的流出(chū)系數基本沒(mei)有變化,這👌是(shi)因爲孔闆厚(hou)度的變化并(bìng)沒有對孔闆(pan)附🏃🏻♂️近的流場(chang)産生影響。Singh[16]也(ye)得出了類似(sì)的結論,根據(jù)他的數值計(jì)算結果,在β=0.4~0.6,Re=1.5×104~1.0×106時(shi),當孔闆厚度(dù)🈲由0.0875D增加到0.225D,流(liú)出系數平均(jun)變化最大🌈不(bu)超過0.52%。相比于(yu)标準孔闆流(liú)量計,槽式孔(kong)闆流量計對(dui)孔闆厚度的(de)變化🌂更敏感(gan),由圖8~圖10可以(yǐ)♌發現,當孔闆(pǎn)厚度由0.05D增加(jia)到0.12D時,槽式孔(kǒng)闆流量計的(de)流出系數明(míng)顯變大,當β=0.4,0.5和(he)0.6時,在雷諾數(shù)從30000到90000的範圍(wei)🐉内,Cp分别平均(jun)增大了4.31%~6.04%,4.92%~6.66%和5.87%~7.57%。流(liú)出系數增🌂大(dà)的原因可以(yǐ)通過圖5和圖(tú)7中的流場分(fèn)布來解釋,即(jí)随着孔闆厚(hòu)度的增加,孔(kong)闆下遊速度(du)在減小,這會(hui)減小💔速度梯(ti)度和各層間(jiān)的剪切應力(li),從而減小流(liú)體流過孔闆(pǎn)時的機♻️械能(neng)損失,進而導(dao)緻更低的壓(yā)降。當孔闆厚(hou)度由0.12D繼續增(zēng)大🌐到0.18D時,流出(chu)系數的變💚化(huà)較小。對于β=0.4的(de)🐕流量計,流出(chū)系數基本沒(méi)有變化;對于(yu)β=0.4和0.5的槽式孔(kong)闆流量計,在(zai)雷諾數30000到90000的(de)範圍内,流出(chū)系數分✨别增(zēng)大了0~0.87%和0.33%~1.79%。可見(jian),直徑比越大(dà),槽式孔闆流(liu)量計對孔闆(pǎn)厚度的變化(hua)越敏感。
4結論(lun)
通過數值模(mó)拟的方法研(yan)究了孔闆厚(hou)度對槽式孔(kǒng)闆流量計内(nèi)部流場及流(liu)出系數的影(yǐng)響,在較大的(de)雷諾數範🈚圍(wei)内,預測⁉️結果(guo)和經驗公式(shi)吻合較好。
1) 相(xiàng)比于标準孔(kǒng)闆,流體流過(guo)槽式孔闆時(shí)下遊的速度(dù)🛀🏻和回流區📞更(geng)小,壓力損失(shī)也更小,所以(yǐ)槽式孔闆流(liú)量計的流出(chu)💞系數🥰大于标(biao)準孔闆流量(liang)計。
2)孔闆厚度(dù)對标準孔闆(pǎn)流量計的内(nei)部流場及流(liú)出系數幾乎(hū)🤩沒有影響。.
3)相(xiàng)比于标準孔(kǒng)闆流量計,槽(cao)式孔闆流量(liàng)計對孔闆厚(hòu)🏒度的變化更(geng)敏感。随着孔(kong)闆厚度的增(zēng)加,槽式孔闆(pǎn)下遊速度減(jian)小,通過孔闆(pǎn)時的壓力損(sun)失變小,流出(chu)系數變大。此(cǐ)外,β越大,槽式(shi)孔♊闆流量計(jì)的流出系數(shu)對孔闆厚度(dù)的變化越敏(min)感,在本文的(de)研究範圍内(nei),當孔闆厚度(dù)由0.05D增加到0.12D時(shi),β=0.4,0.5,0.6的槽式孔👄闆(pan)流量計的流(liu)出系數分别(bie)👉增大了4.31%~6.04%,4.92%~6.66%,5.87%~7.57%。當孔(kong)闆厚度由0.12D繼(jì)續增✌️大到0.18D時(shí),β=0.4的流量計流(liú)出系數基本(ben)不變,而β=0.5和0.6的(de)流量計流出(chū)👨❤️👨系數分别增(zeng)大了0~0.87%和0.33%~1.79%。
以上(shang)内容源于網(wǎng)絡,如有侵權(quan)聯系即删除(chú)!











