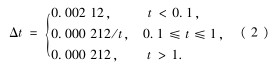在流(liú)體機械瞬态流(liú)動的過程中,需(xū)要對瞬時流量(liàng)進行測🏒試．電磁(cí)流量計在測量(liàng)快速變化的流(liú)量時,其轉換器(qi)的信号處理時(shí)間普遍超🐉過0．２s,需(xu)要經過特殊設(she)計才能達到要(yao)求[5];渦輪流量計(jì)在測試小流量(liàng)的瞬時變化時(shi),存在強烈的非(fēi)線性問題．而在(zai)許多場合,孔闆(pǎn)流量計能較好(hao)地用于瞬态流(liu)量的測試．
　　基于(yú)CFD技術,通過改變(bian)流量﹑直徑比﹑孔(kong)闆厚度和流體(tǐ)介🏃🏻‍♂️質等‼️,對孔闆(pǎn)内部穩定流動(dòng)進行了研究．采(cai)用CFD技術研究了(le)方形孔和圓形(xíng)孔闆流量計在(zài)測量濕夭然氣(qi)時的異同;對錐(zhuī)體流量計的孔(kong)流系數🏃🏻‍♂️進行數(shu)值模拟;對周期(qi)性波動的流量(liang)流經孔闆進行(háng)了實驗和理論(lùn)分析後指出,孔(kǒng)闆前後壓差呈(cheng)現非線性,且滞(zhì)後于流量的🔞變(bian)化,稱之爲“渦慣(guan)性”．
　　鑒于目前未(wèi)見有對孔闆流(liu)量計在測量流(liú)量加速瞬态過(guo)程的相關研究(jiu),爲了從内流角(jiao)度揭示壓差滞(zhì)後于流量變化(hua)的原因,考妞到(dao)采用試驗測量(liang)較爲困難,文中(zhong)采用CFD方法分别(bié)對穩态和加速(sù)過程的孔流系(xi)數進行數值預(yu)測,重點分析孔(kǒng)流系數與流動(dòng)狀态瞬時轉變(bian)間的聯系,爲實(shí)現采用孔闆流(liú)量計測量瞬時(shi)流量提供參考(kao)。
1物理模型和數(shù)值方法
1.1基本理(lǐ)論
　　孔闆流量計(jì)是一種差壓式(shi)流量計．對于不(bu)可壓流體的水(shuǐ)平管🎯流動,忽略(lue)管壁摩擦阻力(lì)損失,根據流體(ti)的連續性和機(jī)械能的相互轉(zhuǎn)化可得

1.2模型﹑網(wǎng)格和邊界條件(jiàn)
　　圖1爲孔闆流量(liang)計的物理模型(xing)示意.根據标準(zhun)孔闆流量計的(de)💘安裝,圖1a中,上下(xià)遊直管段長分(fen)别取10D和5D作爲穩(wen)定直管段.其中(zhōng)上下遊管内徑(jìng)D取100mm,孔闆厚度δ取(qǔ)3mm.
　　流量從0以恒定(dìng)加速度增長,如(rú)圖1b所示;測壓點(dian)的位置示♊于圖(tú)☔1c.

　　爲了準确捕捉(zhuō)孔闆前後流場(chang)的變化情況,首(shou)先在壁面附🎯近(jin)劃分了邊界層(ceng)網格,邊界層第(dì)1層厚度爲0.1mm,共10層(céng),高度增長因子(zi)爲1.1;其次,用與孔(kǒng)闆等孔徑的圓(yuan)柱面作爲分界(jiè)面,對内部流域(yù)進行切割,并對(dui)該邊界面附近(jin)劃分同上☎️的邊(bian)界層💘網格,其内(nèi)部區域采用蝶(dié)形網格劃分;最(zuì)後,在邊界層設(shè)置好的基礎上(shang)🍓,采用結構化網(wang)格生成方式完(wan)成其餘部分的(de)網格劃分.
　　圖２給(gei)出了孔闆附近(jin)的網格分布.以(yǐ)常溫狀态下液(yè)🧑🏾‍🤝‍🧑🏼态水🛀🏻作爲流體(ti)介質,動量﹑湍動(dòng)能和湍流耗散(san)率方🔱程的離散(san)選擇二階迎風(feng)♈格式,壓力和速(su)度耦合選用SＩMＰLＥ算(suan)法,穩态和加速(sù)條件下的⭐湍流(liú)模🏃‍♀️型分别采用(yòng)Realizablek－ε和RealizableDＥS模型.穩态和(hé)加速過程的進(jìn)口均采用♊速度(du)進口邊界條件(jian),流體加速曲線(xiàn)見圖1b,管壁爲無(wú)滑移壁面邊界(jie)條件.

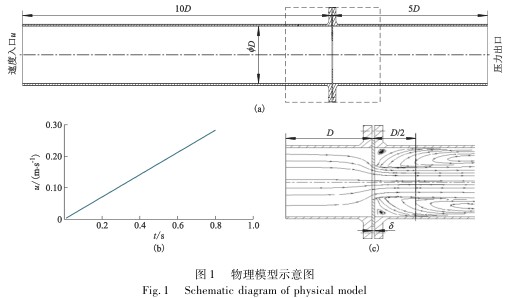
　　由于流速(sù)不斷增大,考妞(niu)采用變時間步(bù)長的方式以提(tí)⭕高叠代🏒過程的(de)經濟性,時間步(bù)長△t與時刻t采用(yong)式(1)的關系式:

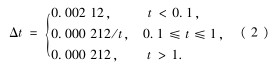
　　流(liu)場求解軟件爲(wèi)Liｎux平台下的Flueｎｔ6．3,采用(yong)曙光1800工作站上(shang)的8個ＩｎｔelXeoｎ處理器🔅(3．２GHz)進(jin)行并行計算,穩(wěn)态叠代4000次約需(xu)２h,瞬态叠代２50個時(shi)間步約需２２h．
2結果(guǒ)分析
2.1孔流系數(shu)和壓降
　　圖3給出(chū)了孔流系數的(de)數值模拟結果(guo),Realiza-blek－ε模拟的穩态孔(kong)流系數C0與ＩSO試驗(yàn)回歸曲線[10]的最(zui)大誤差在3％以内(nei),标準k－ε的最大誤(wù)差達6％[6]．
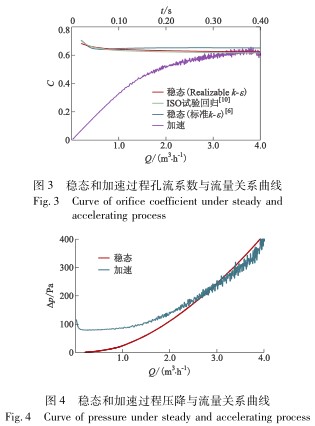
　　對于流量(liàng)Q≤0．6m3/h,C0随流量的增加(jia)緩慢下降,之後(hou)保持在0．63左右．與(yu)C0不🈲同的是,C從0開(kai)始随流量的增(zeng)大而增大,并逐(zhú)漸向🆚C0靠近,直至(zhi)Q≥3．5m3/h後才達到C0的水(shuǐ)平．C在時間上滞(zhi)後于C0．圖4中△p－Q曲線(xian)顯示,Q≤3．0m3/h時,加速過(guò)程孔闆前後壓(yā)降高于同等流(liú)量下穩态壓降(jiang);Q≥3．0m3/h後,瞬态壓降才(cai)降爲穩态水平(ping)．

2.2速度和壓力場(chang)分析
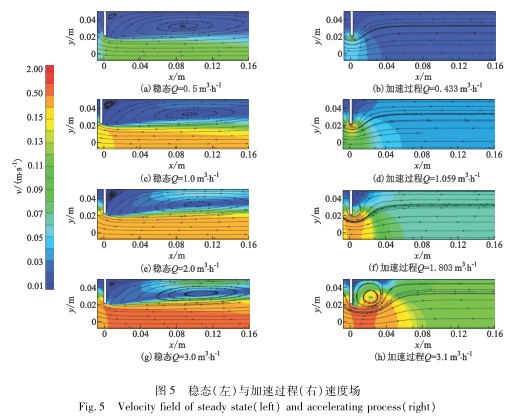
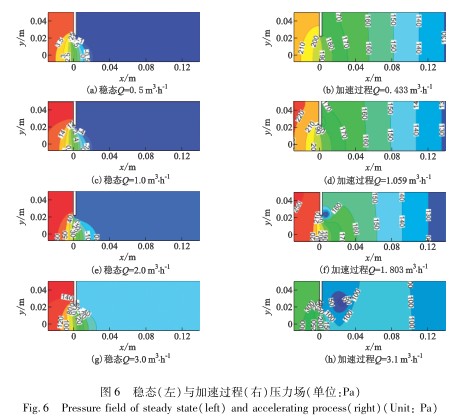
　　從内流角(jiǎo)度分析導緻第(dì)２．1節中C和C0不同的(de)原因,圖5和圖6分(fen)别😄給出并對比(bǐ)了相同流量下(xia)穩态和加速過(guo)程中流經孔闆(pan)前後✔️流體的速(sù)度和壓力場．對(duì)于Q≤3．0m3/h穩态條件☔,孔(kong)闆後方始終可(kě)觀察到一個被(bèi)拉長的主渦和(he)孔闆右上方的(de)小渦,流動的損(sun)失較大,同時表(biao)明流場中已形(xíng)成穩定的🔞流動(dong)通道,動能和壓(ya)能的轉化已達(da)到平衡,流動的(de)損失(長漩渦)也(yě)趨于穩定,并且(qie)壓差随流量的(de)增大而穩定增(zēng)大．
　　加速過程中(zhong)孔闆後方的漩(xuán)渦是逐漸形成(cheng)的:小流量時流(liú)動較爲平穩,流(liu)體不斷被加速(sù)的流體向下遊(yóu)推動,漩渦來☎️不(bu)及形成,流動的(de)損失較小;随着(zhe)流量的不斷加(jia)大,孔闆後方開(kāi)始出現流動分(fèn)離(約在Q＞1．1m3/h時);當流(liu)量進一步加大(dà),孔闆後方出現(xiàn)了較大的漩渦(wo)．加速前期,壓力(li)沿整個管道逐(zhú)漸向✔️下遊傳播(bō),壓能傳播的距(ju)離較長,沒有在(zài)短距離内快速(su)轉換爲動能．
經(jing)上述分析可以(yi)認爲,導緻加速(sù)前期C和C0之間差(chà)異的内流原因(yin)是,漩渦形成的(de)滞後以及加速(sù)前期壓🏒力能❄️沒(méi)有在短距離内(nèi)全♈部轉化爲動(dong)能．
　　随着流量的(de)增大,孔闆後方(fang)出現了明顯的(de)漩渦,漩渦中心(xīn)附近💛區域即爲(wèi)低壓區．雖然孔(kong)流系數和壓降(jiang)的瞬态和穩态(tài)值分别相互接(jie)近,然而由于流(liú)體仍然處于加(jiā)速階段,因此流(liú)動狀态(漩渦的(de)形狀和位置)和(he)壓力分布與穩(wěn)态條件相比,仍(reng)然存在較大差(chà)異．


3結論
　　通過CFD技(jì)術,實現了穩态(tai)和加速流體流(liu)經孔闆後流場(chang)的數值模拟,得(de)到了孔流系數(shù)﹑流場和壓力的(de)模拟結果,主要(yào)概❓括爲:
1)穩态孔(kǒng)流系數C0的數值(zhi)預測值與ＩSO試驗(yan)回歸曲線十分(fèn)接近🛀🏻,Realizablek－ε比标準k－ε的(de)C0預測值更接近(jin)ＩSO試驗回歸曲線(xiàn),誤差分别爲3％和(hé)6％;
２)加速過程,C随流(liú)量的增大逐漸(jian)增大并靠近穩(wen)态C0;加速前期,壓(ya)🔆差高于穩态水(shui)平,随着流量的(de)不斷增大,瞬态(tài)和穩态壓🔱差相(xiàng)互接🔞近．3)導緻加(jia)速前期C和C0之間(jian)差異的内流原(yuan)因是,漩渦形成(cheng)的滞後以及加(jiā)速前期壓力能(neng)沒有在短距離(lí)内全👄部轉化爲(wèi)動能．文中内容(róng)可爲利用孔闆(pǎn)流量計測量瞬(shùn)時流量提供參(can)🌈考依據,爲流體(tǐ)機械内部非定(ding)常流動等特殊(shū)問題的提供基(ji)🥵本保障．今後的(de)工作将圍繞流(liú)量波動﹑階躍和(he)突減等其他瞬(shùn)🐉态狀況．

以上内(nei)容來源于網絡(luo)，如有侵權請聯(lián)系即删除!