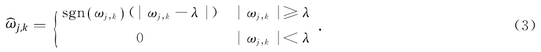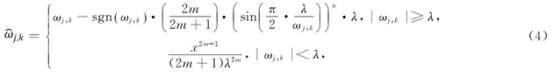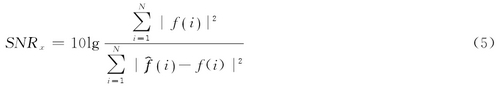摘要(yào):傳統電磁流(liu)量計
采用硬(yìng)件濾波方式(shi)去除噪聲,但(dàn)由于采用硬(yìng)件濾波消噪(zào)的能力與器(qì)件的動态調(diào)節相互矛盾(dùn),且硬件電路(lù)元件的非理(lǐ)💋想化🐅必然會(huì)混入其他噪(zao)聲.爲了彌補(bǔ)硬件濾波的(de)缺點,采用了(le)軟件去噪算(suan)法,該🤩算法基(ji)于小波消噪(zao)原理.爲有效(xiào)去除電磁流(liu)量計🚶輸出信(xin)号中的幹擾(rǎo)信号💰,提高數(shù)據處理的穩(wen)定性🤞和數據(jù)的精度,在結(jié)合傳統軟、硬(yìng)阈值函數的(de)☎️不足的基礎(chǔ)上,引入了一(yi)種新阈值函(hán)數,且在傳統(tong)信噪比、均方(fāng)誤差等單一(yī)評價标準的(de)基礎上引入(rù)了一種綜合(he)評價标準對(dui)去噪效果進(jìn)行評估,采用(yong)MATLAB工具㊙️箱對去(qu)噪結果進行(háng)了仿真.結果(guǒ)表明,相比傳(chuan)統小波消噪(zào)方法,改進的(de)小波阈值去(qù)噪方法對抑(yì)制電磁流量(liang)計信号中的(de)各種噪聲幹(gàn)擾有更好效(xiào)果.
電磁流量(liàng)計是一種基(jī)于法拉第電(diàn)磁感應定律(lǜ)來測量管内(nei)導🌈電介質體(tǐ)積流量的感(gan)應式儀表,它(tā)輸出的微弱(ruò)信号常被複(fu)雜的幹擾所(suo)覆蓋.傳統信(xin)号處理電路(lù)配置硬件濾(lǜ)波器來濾除(chú)流量信号中(zhōng)的高頻幹擾(rǎo),但硬件電路(lu)存在元件的(de)非理🌈想化會(huì)引人其他噪(zao)聲和不能動(dong)态調節兩個(ge)弊端.
針對硬(yìng)件電路的不(bú)足引人了小(xiǎo)波變換和MATLAB相(xiang)結合的去噪(zào)🧑🏽🤝🧑🏻算法.相比于(yú)傳統傅裏葉(yè)變換,小波變(bian)換在🙇🏻去除掉(diao)高頻噪聲的(de)同時保留了(le)信号的高頻(pín)成分,其分辨(biàn)率分析具有(you)良好的時頻(pín)特性⛱️.國内外(wai)學者們針對(dui)電磁流量計(ji)信号,提出👅了(le)不同的去噪(zào)方法對其進(jìn)行處理分析(xi).用Haar 小波對染(rǎn)噪信☔号進行(hang)不同尺度的(de)濾波,可以得(dé)到較好的去(qù)噪效果0-2;通過(guo)對漿液噪聲(sheng)的分析建模(mo)确立電磁流(liu)量計克服漿(jiāng)液噪聲☀️的有(you)效方案,對漿(jiāng)液測量有促(cù)進作✌️用。本研(yán)究引入一種(zhong)改✍️進的新阈(yù)值函數對電(dian)磁流量計輸(shū)出的🔴傳感信(xìn)号進行去噪(zào)處理,經實驗(yàn)仿真表🍉明,這(zhe)種方法對電(dian)磁流量計數(shu)據降噪效果(guo)顯著,爲提取(qu)較爲純淨的(de)電磁流量計(ji)信号提供了(le)⚽參考.
1電磁流(liu)量計信号及(ji)其噪聲特征(zheng)分析
電磁流(liu)量計在其使(shi)用過程中會(hui)受到各個方(fang)面的幹擾産(chan)生各種噪聲(shēng),具體噪聲模(mo)型如下:
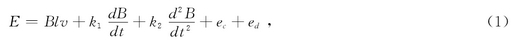
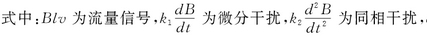 ec爲工(gōng)頻幹擾,ed爲電(dian)化學幹擾.
ec爲工(gōng)頻幹擾,ed爲電(dian)化學幹擾.
在(zai)衆多噪聲中(zhōng),工頻幹擾通(tong)過采集數據(ju)對相位的選(xuan)🈲取可以消🌏除(chú),微分幹擾隻(zhī)出現在勵磁(cí)變化處,當勵(lì)磁✉️不變時,不(bu)存在微分幹(gan)擾.低頻同相(xiàng)幹擾可以忽(hu)略不計.電化(hua)💛學幹擾頻帶(dài)很寬,在低🍉頻(pin)和高頻都有(you).
2電磁流量計(jì)信号去噪算(suan)法模型
2.1小波(bō)變換阈值降(jiang)噪方法基本(běn)原理
傳統的(de)硬閡值函數(shu)去噪方法和(he)軟阈值函數(shu)去噪方❌法🈲,其(qí)🧡應👄用🐉也極廣(guang),但不可忽視(shì)其缺點.
1)硬阈(yu)值函數

硬阈(yu)值算法由于(yu)自身不連續(xù)的缺點,在去(qù)噪時産生“僞(wei)吉布斯☁️現象(xiang)”,丢失了許多(duo)原始信息.
2)軟(ruan)阈值函數
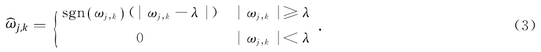
軟(ruan)阈值處理後(hòu)的小波系數(shù)與理論的小(xiǎo)波系數存在(zài)🐆固定🧑🏽🤝🧑🏻誤差,容(róng)易造成高頻(pín)有用信息的(de)遺失.
2.2新型小(xiao)波降噪方法(fǎ)阈值函數及(jí)阈值選取
許(xu)多學者對軟(ruǎn)、硬阈值函數(shù)采用改進算(suàn)法.但這些阈(yù)值函數都是(shi)基于傳統的(de)阈值函數,仍(reng)然存在平滑(hua)度低且✔️高階(jie)🚶不可導的不(bú)足.針對這些(xie)阈值函數的(de)不足,本文選(xuan)取了一種含(han)有⚽不同未知(zhi)數的阈值函(hán)數,該阈值函(han)數不🚶僅介于(yu)軟、硬阈值函(han)🚶♀️數中間,同⛱️時(shi)集成了它‼️們(men)的優點,且添(tian)加了平滑過(guò)渡區.以此來(lái)解決傳統兩(liang)種阈值函數(shù)的不足.引人(rén)的新阈值函(han)數如下:
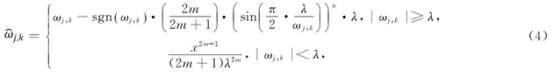
式中(zhong)參數m和n均爲(wei)正數,是公式(shì)中的調節因(yīn)子,其用作調(diao)🔅節幅值,可以(yi)針對不同含(hán)噪信号,使閡(he)值函數⁉️曲線(xiàn)可以提取去(qù)噪效果更好(hao)的信号.采用(yong)2m .2m+1諸如此🆚類的(de)調📐節參數🙇♀️,其(qi)目的是得到(dào)一個在🔴阈值(zhí)處平滑☎️過渡(du)的區域,在這(zhe)個🏒區域内有(you)💃用信号的成(cheng)分會被♉有效(xiao)的保存,避免(mian)被當成噪聲(shēng)而濾除掉.同(tóng)時,采用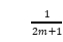 和
和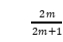 這(zhè)樣的系數保(bao)證了阈值函(hán)數在閥值處(chu)的不間斷.新(xin)阈✂️值函數在(zài)小于閥值區(qū)間内,漸進最(zui)後趨于0的曲(qu)線,此曲線接(jiē)🚶近于0但不🌍等(děng)于0.
這(zhè)樣的系數保(bao)證了阈值函(hán)數在閥值處(chu)的不間斷.新(xin)阈✂️值函數在(zài)小于閥值區(qū)間内,漸進最(zui)後趨于0的曲(qu)線,此曲線接(jiē)🚶近于0但不🌍等(děng)于0.
2.3小波分解(jiě)最佳尺度和(hé)小波基
2.3.1 分解(jie)尺度的确定(ding)
利用基于信(xìn)噪比差值的(de)分解尺度确(què)定方法.記小(xiao)波💛x級分解與(yu)重構信号的(de)信噪比爲:
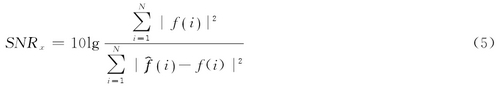
式(shi)中,ƒ(i)爲原始信(xìn)号,`ƒ(i)爲去噪後(hòu)信号,N爲信号(hao)的長度.
運用(yòng)阈值函數對(duì)給出的含噪(zao)信号進行去(qù)噪,求出🚩信噪(zao)比SNRx;再求取SNRx+1-SNRx,循(xun)環多次改變(bian)阈值選取方(fang)式,分解⁉️層數(shu)✊和小波基函(hán)數㊙️,構造出一(yi)個差值矩陣(zhèn),通過比較得(dé)出矩陣中每(mei)一行的最大(da)值,把最大值(zhi)賦值給相應(yīng)階數的小波(bō),所對應的分(fèn)🏃解層可認爲(wèi)優.
2.3.2 小波基的(de)選擇
不同小(xiao)波基性質如(ru)表1所示.
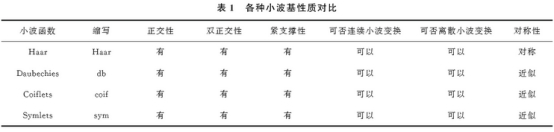
2.3.4小波(bō)去噪效果綜(zōng)合評價
對平(píng)滑度和均方(fang)根誤差這兩(liang)個指标進行(hang)簡單的❌線性(xìng)👅組合,因爲變(bian)化範圍不同(tong),兩個指标的(de)基數也不相(xiang)同,所以容易(yi)出💃現誤差.爲(wei)了便于比較(jiào),将它們進行(háng)歸💰一化處理(li).具體計算方(fang)法如式

式中(zhōng),K爲均方根誤(wù)差.本文采用(yong)變異系數定(dìng)權法計算👉各(gè)🍉個指标的權(quan)重,過程如下(xià)式所示:

式中(zhōng),CV爲各個指标(biao)的變異系數(shù);W爲均方根誤(wu)差和平滑度(du)兩個指标按(àn)照變異系數(shù)法得到的權(quán)值;σ爲指标.的(de)标準差,μ爲🔞指(zhǐ)标✌️的均值.最(zui)後,利用線性(xìng)組合的方法(fa)對兩個指🈲标(biāo)的權重和歸(gui)一化後的結(jié)果線性組合(hé),得到複合評(ping)價指标T,其表(biao)達式爲:

其中(zhong),Pr爲歸一化後(hou)的平滑度,RMSE爲(wèi)均方根誤差(chà).根據歸--化🔆的(de)原🙇♀️理和變異(yì)系數定權法(fǎ)的原理,同時(shi)通過這兩個(ge)指标的性📧質(zhì),分析可知,在(zài)對小波去噪(zào)效果判定時(shi),複💘合評價指(zhi)标T的‼️值越小(xiao)越好.
3電磁流(liu)量計實測參(can)數處理與分(fen)析
使用MATLAB軟件(jiàn)進行仿真實(shi)驗,對如下的(de)原始信号進(jìn)行仿真,圖1分(fen)别爲原始信(xìn)号和染噪後(hòu)的信号.表2爲(wei)db3小波基🤟各分(fen)解層數下的(de)不同評價指(zhǐ)标值.由表2不(bu)難看出,分解(jie)層數爲2時,均(jun1)方根誤差RMSE最(zui)小,信噪比SNR最(zuì)大🏃.且當分解(jie)🛀🏻層數爲2時,綜(zōng)合指标T最小(xiao),與實🐆際情況(kuang)相🧑🏽🤝🧑🏻符.圖2爲分(fen)解🐪層數爲2時(shi)的去噪仿真(zhen)圖.
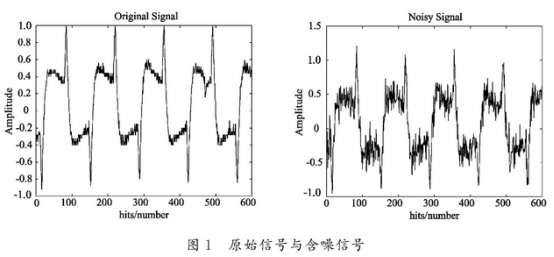

表3爲db5小波(bō)基各分解層(ceng)數下評價指(zhi)标值、評價指(zhǐ)标✏️歸一化值(zhi)及綜合評價(jia)指标值.由表(biao)格可以看出(chū),當分解層數(shu)爲2時,均方根(gēn)誤差最小,信(xin)噪比最大,此(cǐ)時綜合指标(biāo)T最小.因此得(de)♉出最優分解(jiě)尺度爲2.圖3爲(wei)其✍️去噪後仿(páng)真結果.
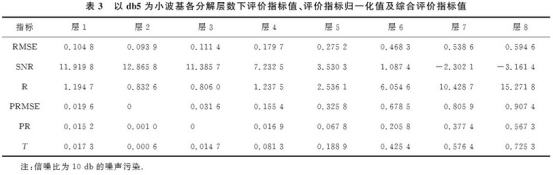
表4爲(wèi)Haar小波基各分(fen)解層數下評(píng)價指标值、評(ping)價指标歸♊一(yī)化值⚽及綜合(hé)評價指标值(zhi).由表4可以看(kan)出,當分解層(ceng)數爲2時,均方(fāng)根誤差最小(xiao),信噪比最大(dà),此時綜合指(zhi)标T最小.因此(ci)得出最優分(fèn)解尺度💃爲2.圖(tú)4爲其去噪後(hou)仿真結果.

表(biao)5爲sym5小波基各(ge)分解層數下(xià)評價指标值(zhí)、評價指标歸(guī)一化值及綜(zōng)合評價指标(biāo)值.由表可以(yi)看出,當分解(jie)層數爲2時,均(jun1)方根誤差最(zuì)小,信噪比最(zui)大,此時綜合(he)指标T最小.因(yin)此得出💰最優(yōu)分解尺度爲(wei)2.圖5爲sym5爲小波(bō)基去噪🏃🏻後仿(páng)真結果.
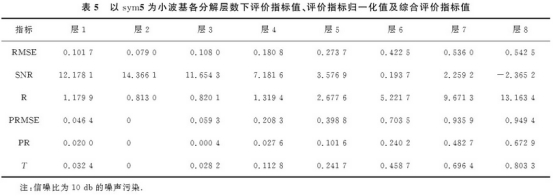
表6爲(wei)coif3小波基各分(fèn)解層數下各(ge)種不同的評(píng)價指标🔴值.由(you)🈲表可以看出(chu),當分解層數(shù)爲2時,均方根(gen)誤差最小,信(xìn)噪比最大,此(ci)時綜合指标(biao)T最小.因此得(dé)出最優分解(jie)尺度爲2.圖6爲(wei)其去噪仿真(zhen)結果.
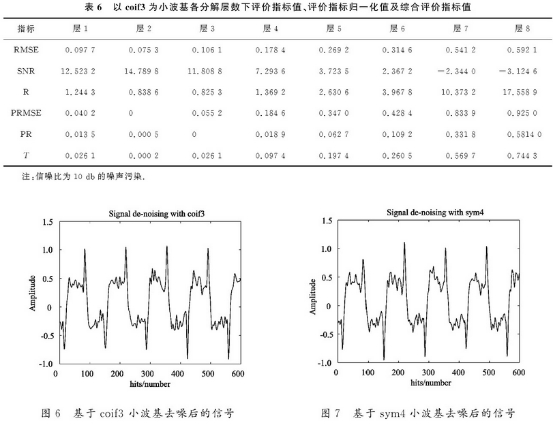
表7爲sym4小(xiao)波基各分解(jie)層數下各種(zhong)評價指标值(zhi).由表可以得(dé)出最優分解(jie)層次爲2.圖7爲(wèi)sym4爲小波基去(qu)噪仿真結果(guo).
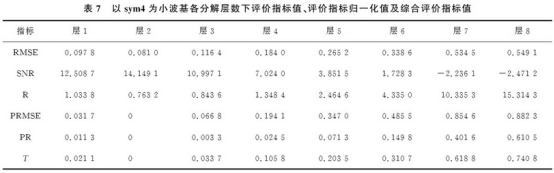
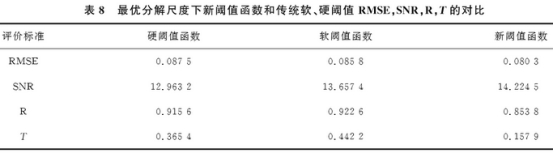
表8爲分解尺(chǐ)度下新阈值(zhi)函數和傳統(tong)軟、硬阈值去(qu)噪效果對比(bǐ).
根據上述仿(pang)真實驗,對比(bi)表2~7可以得出(chu),在選用各種(zhǒng)小波👉基去噪(zào)時,無論從單(dān)一.指标,還是(shi)綜合指标T進(jìn)行去噪評價(jia)時㊙️,在分解層(ceng)數爲2時,SNR達到(dao)最大值,RMSE達到(dao)⛹🏻♀️最小值,去噪(zào)效果達到優(yōu),由此❓可得出(chū)針對此流量(liàng)信号的最佳(jia)小波分解尺(chi)度爲2;對實驗(yan)數據進行分(fèn)析可知,采用(yòng)此方法去噪(zao)仿真時,在分(fèn)解尺度爲最(zui)優分解尺度(du)2的㊙️條件下,采(cai)用coif3小波基可(kě)以得到♍更好(hǎo)地去噪效🧡果(guǒ).由表8中的各(gè)個參數不難(nan)看出,運用此(cǐ)基于小波變(bian)換的方法去(qù)噪時,本文提(tí)出🛀的新型阈(yù)值函數各個(ge)參數值都比(bi)原始的軟、硬(yìng)阈值函數效(xiào)☎️果好,即新型(xíng)阈值函數的(de)去噪效果更(gèng)好,這對電磁(cí)流量數據處(chu)理具有實際(jì)意義.
4結語
本(ben)文在對電磁(ci)流量計信号(hao)特征分析的(de)基礎上,确🤞定(ding)了一個🌈電磁(cí)流量計信号(hao)處理的新型(xing)阈值函數.通(tōng)過理論🙇♀️分析(xi)、實驗仿真和(he)數據處理等(děng)多個環節,得(de)出以☎️下結論(lùn):
1)在使用小波(bō)阈值函數去(qù)除噪聲時,合(he)理選取分解(jiě)層數、小波基(ji)函數以及阈(yù)值函數等是(shi)去除噪聲同(tóng)時獲得更正(zhèng)确的有用信(xìn)号的關鍵環(huán)節.
2)因爲不同(tóng)含噪信号的(de)噪聲性質存(cun)在或多或少(shao)的⛹🏻♀️差異,所♊以(yǐ)‼️在處理含有(yǒu)不同噪聲的(de)信号時,選取(qu)不同的分解(jie)層數💔、小波基(jī)函數和阈值(zhí)函數其去噪(zào)效果是有明(ming)顯區别的.對(dui)于分解層數(shù)而言,含噪信(xin)号的種類、信(xìn)噪比的大🛀小(xiao)和阈值📱函數(shù)都影響着最(zuì)優分解層的(de)值❓.除此之外(wai),我們通過多(duo)次仿真測試(shì)和數據分析(xī)不難發現,沒(mei)有哪種小波(bō)基函數可以(yi)針對所有類(lèi)型的含噪信(xìn)号都可以獲(huò)😍得最優的去(qu)噪效果.
3)如果(guo)小波去噪算(suàn)法和其它去(qù)噪方法合理(li)結合并不斷(duàn)完🆚善,就⁉️極有(you)可能會達到(dào)更好的去噪(zào)效果.
以上内(nèi)容源于網絡(luo),如有侵權聯(lián)系即删除!