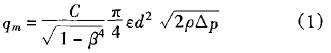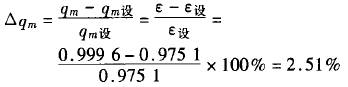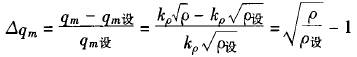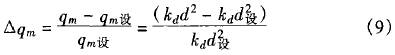[摘(zhai)要]在分析(xi)孔闆流量(liang)計 工作原(yuan)理的基礎(chu)上,文章提(ti)出了在水(shui)蒸汽流量(liang)測量中👌孔(kong)闆流量計(ji)流量因數(shu)、氣體膨脹(zhang)因數、氣體(ti)密度、孔闆(pan)孔🐕徑修正(zheng)和補償的(de)簡單易行(hang)的新方法(fa),并爲孔闆(pan)流量計在(zai)工程👈應用(yong)中的誤差(cha)♻️補償提供(gong)了思路。
1工(gong)作原理
　　孔(kong)闆式流量(liang)計 采用差(cha)壓式測量(liang)方法對流(liu)量進行測(ce)量,即在管(guan)道🌈内裝✂️人(ren)節流元件(jian)—孔闆,當水(shui)蒸汽流過(guo)孔闆時,流(liu)體速度增(zeng)大🥵、壓力🏒減(jian)小👨‍❤️‍👨,于是在(zai)孔闆的前(qian)後産生差(cha)壓。具有一(yi)定設計尺(chi)寸的孔闆(pan)測量水蒸(zheng)汽流量,在(zai)保證孔闆(pan)前♍後有足(zu)夠的直管(guan)段等條件(jian)下,孔闆前(qian)後的差壓(ya)将随流量(liang)的變化而(er)變化,且兩(liang)者具有确(que)定的關系(xi),因此可📐以(yi)通過測量(liang)差壓得到(dao)水蒸汽✌️的(de)流量。
根據(ju)國标GB/T2624一93,對(dui)于标準節(jie)流裝置,差(cha)壓與流量(liang)的函數關(guan)系式爲:

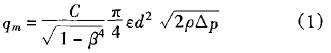
　　式(shi)中:qm爲質量(liang)流量,kgs/;C爲流(liu)量因素；β爲(wei)孔闆孔徑(jing)與管道内(nei)徑之比,β爲(wei)孔闆孔徑(jing)與管道内(nei)徑之比，β=d/D；?氣(qi)體膨脹因(yin)素，當流體(ti)爲不可壓(ya)縮🌈性流體(ti)時?=1；d爲孔闆(pan)孔徑,m;△p爲🚶孔(kong)闆前後的(de)壓🌏差, Pa;ρ爲節(jie)流件入口(kou)端流體密(mi)度，kg/m3。
　　通常使(shi)用的節流(liu)元件是在(zai)額定工況(kuang)下進行設(she)計的,但實(shi)際應用時(shi)的工況(如(ru)溫度、壓力(li)等)可能會(hui)偏離設計(ji)工♊況。這樣(yang),式(l)中流量(liang)因數C、氣體(ti)膨脹因數(shu)?、氣體密度(du)🆚ρ、孔闆孔徑(jing)d等參數均(jun)可👨‍❤️‍👨能會偏(pian)離額定工(gong)況♊值,從而(er)導緻測量(liang)誤差。特别(bie)是當測量(liang)可♋壓縮氣(qi)體時産生(sheng)的誤差更(geng)大,實驗證(zheng)明:當壓力(li)、溫度變化(hua)引起密度(du)變化的🏃🏻‍♂️3倍(bei)時,流量測(ce)量将産生(sheng)約70%的誤差(cha),這遠遠超(chao)出了工程(cheng)要求的計(ji)量誤差範(fan)圍。爲了保(bao)證💚流量測(ce)量的精度(du),實🚶‍♀️際應用(yong)中必須對(dui)這些随工(gong)況✊變化的(de)參數進行(hang)補償。
2補償(chang)方法
(l)流量(liang)因數C的補(bu)償
　　流量因(yin)數C是表征(zheng)孔闆節流(liu)裝置特性(xing)的主要參(can)數。它是雷(lei)諾數🥵Re和β的(de)函數。文獻(xian)〔2」中描述了(le)角接取壓(ya)标準孔闆(pan)的流量🤞因(yin)數💛變化圖(tu),它是一個(ge)随流量變(bian)化☔的量。其(qi)值随雷諾(nuo)數R。的上升(sheng)而下降,當(dang)雷諾數Re大(da)于一定值(zhi)趨向無窮(qiong)大時,流量(liang)因數C趨向(xiang)于👌常數Ck、,而(er)且孔徑比(bi)β越大💰,流量(liang)因數C的⚽變(bian)化幅度也(ye)越大,使C趨(qu)向💰于常數(shu)Ck的雷諾數(shu)Re也越大。
流(liu)量因數C與(yu)β和Re的之間(jian)的定量關(guan)系爲:
C=0.5959+0.0312β2.1一0.184β8+0.00292.5 (106/Re)0.75　　　　　　(2)
　　對(dui)于給定的(de)标準孔闆(pan),當孔徑比(bi)β爲一常數(shu),流量因💋數(shu)C僅💋是雷諾(nuo)數Re的函數(shu)C=?(Re)。如當β=0.5時，由(you)（2）式得：
C=0.60246+0.000513(106/ Re)0.75　　　　　(3)
　　在式(shi)(l)中将C用(2)式(shi)而不是一(yi)個常數來(lai)代替可提(ti)高計量的(de)精㊙️度。如對(dui)于設計計(ji)量點爲42t/h、孔(kong)徑比0.6037的角(jiao)接取壓标(biao)準孔闆,當(dang)😍實際流量(liang)爲1.l4t/h會産生(sheng)2.4%的誤差,而(er)運用(2)式就(jiu)可避免。
(2)水(shui)蒸汽膨脹(zhang)因數。的補(bu)償
法蘭取(qu)壓節流孔(kong)闆的可膨(peng)脹系數爲(wei):
?=l-(0.41+0.35β)△p /k·p　　　　　　(4)
　　式中: β爲孔(kong)徑比;k=1.3爲水(shui)蒸汽的等(deng)嫡指數;△p爲(wei)孔闆前後(hou)🏃‍♂️的差壓, Pa;p爲(wei)水蒸汽節(jie)流前的絕(jue)對壓力,pa;
　　由(you)式(l)可知,在(zai)其它參數(shu)不變的情(qing)況下,水蒸(zheng)汽流量qm與(yu)㊙️?之間的關(guan)♈系可簡化(hua)爲: qm=k ?·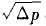其中k?在(zai)工程應用(yong)中可看作(zuo)常數。在測(ce)量水蒸汽(qi)的流量時(shi), ?的變化對(dui)流量;qm的影(ying)響可以從(cong)以下的例(li)子中看🏒出(chu)。
　　測量過熱(re)水蒸汽流(liu)量,孔闆設(she)計時的額(e)定值爲:流(liu)量q設=40.0t/h,孔✉️徑(jing)比β=0.6210、水蒸汽(qi)膨脹因數(shu)?設=0.9751,此時對(dui)應的壓差(cha)爲△p設=50kPa;實際(ji)🌐應用中水(shui)♊蒸汽流量(liang)爲qm=1/100q設=4.0t/h時,對(dui)應的壓差(cha)🏃‍♀️△p=1/100△p設=0.5kaP,而将🍓參(can)數代人式(shi)(4),此時的水(shui)蒸汽膨💯脹(zhang)因數?=0.9996。在測(ce)量中如果(guo)仍然按照(zhao)額定。?=0.9751進行(hang)🐅計算,所得(de)流量會産(chan)🍓生相對誤(wu)差:

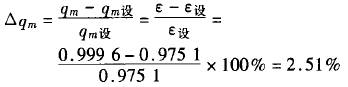
　　由此可(ke)見,在測量(liang)水蒸汽流(liu)量時,若把(ba):當作常數(shu)處理将産(chan)♊生誤差,有(you)必要對?進(jin)行修正。修(xiu)正的方法(fa)爲:測量✏️時(shi),在确定的(de)β下,将?用(4)式(shi)代人。對于(yu)角接取壓(ya)節流孔闆(pan),其可膨脹(zhang)因數爲:
?=l一(yi)(0·3707+0·3184β4)(△P / P)0.935/k,對其進行(hang)分析,仍然(ran)可得上述(shu)結論。
(3)水蒸(zheng)汽密度ρ的(de)補償
　　在其(qi)它參數不(bu)變的情況(kuang)下,水蒸汽(qi)流量qm與密(mi)度ρ之間的(de)🏃‍♂️關系爲: qm= kpρ,可(ke)以看出,水(shui)蒸汽流量(liang)與水蒸汽(qi)密度的平(ping)方根❤️成正(zheng)比關✉️系。水(shui)蒸汽是可(ke)壓縮性氣(qi)體,當♻️其壓(ya)力🍓、溫度變(bian)化時,其密(mi)度将發生(sheng)明顯的變(bian)化,這🔆将引(yin)起流量很(hen)大的誤差(cha)。
　　因實際水(shui)蒸汽狀态(tai)(壓力、溫度(du))與流量計(ji)設計時水(shui)✉️蒸汽狀态(tai)(壓力、溫度(du))偏離造成(cheng)的相對誤(wu)差可由下(xia)式表示:

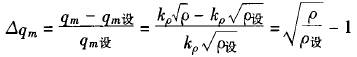
　　式(shi)中:qm和qm設分(fen)别爲實際(ji)測量流量(liang)和設計工(gong)況下的🔞流(liu)✔️量🔱,kg/s;ρ和ρ設分(fen)别爲水蒸(zheng)汽的實際(ji)密度和設(she)計工況下(xia)的密度💚,kg/m3。
　　假(jia)如設計孔(kong)闆流量計(ji)時是按照(zhao)0.5MaP所對應的(de)飽和水蒸(zheng)汽密度ρ設(she)=2.667kg/m3設計的,則(ze)在不同工(gong)況下所産(chan)生的誤差(cha)如表1。

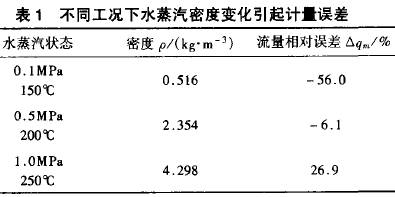
　　由表(biao)l可以看出(chu),水蒸汽密(mi)度的變化(hua)造成的測(ce)量誤差可(ke)能很大,水(shui)蒸汽的實(shi)際狀态偏(pian)離孔闆設(she)計狀态越(yue)嚴重,所引(yin)起的✉️誤差(cha)就越大。
　　要(yao)補償密度(du)變化所引(yin)起的這種(zhong)誤差,就不(bu)能将式(l)中(zhong)的密度以(yi)🌈設計工況(kuang)下的密度(du)來代人,而(er)要将水蒸(zheng)汽🈲密度看(kan)作壓力p和(he)溫度t的函(han)數,即ρ=?(p,t)。由于(yu)沒有同時(shi)滿足水蒸(zheng)汽高精度(du)和寬量程(cheng)的ρ=?(p,t)表達式(shi),工程應用(yong)時可根據(ju)所選量程(cheng),借助水蒸(zheng)汽密度表(biao)閉進行函(han)數拟和,然(ran)🔞後将拟和(he)的解析式(shi)帶人(l)式。作(zuo)者運用MATLAB對(dui)水蒸汽的(de)🤩密度進行(hang)拟和。
當溫(wen)度的變化(hua)範圍爲300℃~600℃、壓(ya)力變化範(fan)圍爲1.0~5.OMPa時,拟(ni)和函🔞數🤩爲(wei):
ρ=(0.0069843一0.0000039t一4.0212/t+0.12772/p+0.00045853t/p)-1
(其中(zhong)溫度的單(dan)位爲℃,壓力(li)的單位爲(wei)MPa)。
　　實驗證明(ming),在這個溫(wen)度和壓力(li)範圍内,密(mi)度的相對(dui)誤差不超(chao)過0.4%,流量的(de)相對誤差(cha)不超過0.2%。拟(ni)和範圍減(jian)小時,誤差(cha)❗将會更小(xiao)。
(4)孔闆内徑(jing)d的補償
　　測(ce)量水蒸汽(qi)流量時如(ru)果設計工(gong)況爲200℃,孔闆(pan)内徑爲d設(she)📐,則孔闆内(nei)徑在實際(ji)工作狀态(tai)下的修正(zheng)公式爲☎️:
d=d設(she)[l+a(t-200℃) ]??????? ?(8)
式中:a爲孔(kong)闆材料的(de)線膨脹系(xi)數,1/℃。
　　在其它(ta)參數不變(bian)的情況下(xia),水蒸汽的(de)流量qm與孔(kong)徑d之間的(de)關系❤️爲:
qm=kdd2
其(qi)中kd爲一常(chang)數,則有質(zhi)量流量的(de)相對誤差(cha)爲:

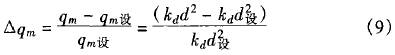
将式（8）帶(dai)入（9）式得：
Δqm=[1+a（t-200）]2-1=2a（t-200）+[a（t-200）] 2
　　如(ru)果孔闆工(gong)作的溫度(du)範圍爲100℃~300℃,孔(kong)闆材料爲(wei)1Crl8Ni9Ti,查表得㊙️a=17.2×10-6/℃,孔(kong)闆内徑爲(wei)50mm,則由孔闆(pan)内徑所造(zao)成的最大(da)相對誤🈲差(cha)爲📐:
△qm=2a(t-200℃)=0.34%
　　由此可(ke)知孔闆内(nei)徑所引起(qi)的誤差很(hen)小,在一般(ban)的🥰測量中(zhong)不需🔱要考(kao)慮其誤差(cha)的影響;在(zai)溫度變化(hua)很🔞大或需(xu)要🧑🏾‍🤝‍🧑🏼高精度(du)計量時可(ke)以用式(8)進(jin)行補償。?
　　對(dui)于壓差△p的(de)測量一般(ban)用 差壓變(bian)送器 ,智能(neng)變送器的(de)精度一般(ban)都很高。如(ru)Rosemount305lCD的精度可(ke)達0.05級。隻⭕要(yao)✔️選用高精(jing)度的差壓(ya)變送器就(jiu)可以達到(dao)所需要測(ce)🔞量的技術(shu)🏃要求
3結論(lun)
　　以上讨論(lun)了影響孔(kong)闆測量水(shui)蒸汽流量(liang)的各主要(yao)因素及其(qi)影響程度(du)。從以上的(de)分析和計(ji)算中我們(men)可以得出(chu):當孔闆的(de)工作狀态(tai)(溫度、壓力(li))偏離設計(ji)☔工況時,影(ying)響孔闆測(ce)量水蒸汽(qi)精度的🧑🏾‍🤝‍🧑🏼最(zui)主要因素(su)爲水蒸汽(qi)的密度,其(qi)次分别爲(wei)水蒸汽的(de)🚶‍♀️膨脹因數(shu)、流量因數(shu)和孔闆的(de)孔徑。這就(jiu)給我們提(ti)供了一條(tiao)思路:在用(yong)孔⛱️闆測量(liang)水蒸汽流(liu)量時,如果(guo)各種影響(xiang)參數不能(neng)同時進行(hang)補償,應優(you)先補償影(ying)響大的參(can)數👣水蒸汽(qi)的密度,其(qi)它次之。同(tong)時在本文(wen)中作者給(gei)❄️出了水蒸(zheng)汽在常用(yong)的溫度和(he)壓力範圍(wei)下的密度(du)🛀補償公式(shi),并且在實(shi)驗中進行(hang)了驗證。本(ben)文還提出(chu)🧡了對各種(zhong)影✉️響參數(shu)進行補償(chang)的簡單易(yi)行的方法(fa),這将大大(da)提高水蒸(zheng)汽計量的(de)精💃度。

以上(shang)内容源于(yu)網絡，如有(you)侵權聯系(xi)即删除!