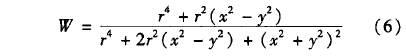摘(zhai)要:采用有(you)限元方法(fa),針對三對(dui)多電極電(dian)磁流量計(ji) 電極在不(bu)同位置時(shi)權重函數(shu)分布情況(kuang)進行數值(zhi)仿真。提出(chu)2個描述權(quan)重函數分(fen)布均勻度(du)的指标:最(zui)大偏差和(he)整體均勻(yun)度,并在電(dian)極數目和(he)位置不同(tong)情況下對(dui)權重函數(shu)的分布情(qing)況進行分(fen)析比較。結(jie)果表明,電(dian)磁流量計(ji)權重函數(shu)分布不僅(jin)與電極數(shu)目有關,還(hai)與電極所(suo)在的位置(zhi)有關。通過(guo)合理設計(ji)電極位置(zhi),三對電極(ji)電磁流量(liang)計在權重(zhong)函數分布(bu)均勻度和(he)平均強度(du)兩方面都(dou)優于單電(dian)極對電磁(ci)流量計。.
1引(yin)言
　　電磁流(liu)量計 是一(yi)種用于導(dao)電性液體(ti)流量測量(liang)的儀表o由(you)于其不受(shou)溫度、壓力(li)、流體密度(du)和粘度等(deng)因素影響(xiang),且其内部(bu)光滑無阻(zu)流部件[3],不(bu)會對流體(ti)産生阻力(li)從而導緻(zhi)壓力損失(shi),因此在工(gong)業生産過(guo)程的流量(liang)測量中得(de)到廣泛應(ying)用。權重函(han)數表示管(guan)道橫截面(mian)上不同位(wei)置流速對(dui)流量計輸(shu)出信号的(de)貢獻大小(xiao),權重函數(shu)均勻則各(ge)點流速貢(gong)獻相同。所(suo)以,在電磁(ci)流量計的(de)設計中,總(zong)是希望權(quan)重函數分(fen)布越均勻(yun)越好。對外(wai)流式電磁(ci)流量計和(he)油管之間(jian)環形區域(yu)的權重函(han)數分布情(qing)況進行了(le)理論推導(dao)和仿真。管(guan)道橫截面(mian)上流體速(su)度呈非軸(zhou)對稱分布(bu)時，采用傳(chuan)統單電極(ji)對電磁流(liu)量計會産(chan)生較大的(de)測量誤差(cha)。而多電極(ji)電磁流量(liang)計可以從(cong)多角度多(duo)位置測量(liang)感應電動(dong)勢,故可用(yong)于非軸對(dui)稱管流流(liu)量的精确(que)測量。
　　目前(qian),對多電極(ji)電磁流量(liang)計權重函(han)數分布情(qing)況的還較(jiao)少。本文多(duo)電極電磁(ci)流量計在(zai)管道橫截(jie)面上權重(zhong)函數的分(fen)布特性。結(jie)果可爲多(duo)電極電磁(ci)流量計傳(chuan)感器的結(jie)構優化提(ti)供進--步的(de)基礎。
2基本(ben)方程與權(quan)重函數
　　當(dang)導電性液(ye)體在磁場(chang)中作切割(ge)磁力線運(yun)動時，液體(ti)中有感應(ying)電流産生(sheng)。根據歐姆(mu)定律有:

　　對(dui)均勻磁場(chang)型電磁流(liu)量計,爲便(bian)于分析和(he)闡明其物(wu)理意義,通(tong)常使用“長(zhang)筒流量計(ji)”物理模型(xing)[13]如圖1所示(shi)，設磁場區(qu)域長度和(he)電極長度(du)均爲2L,此時(shi)電極呈線(xian)狀。當L-→∞時,方(fang)程的求解(jie)就可由三(san)維空間坐(zuo)标問題簡(jian)化成=維平(ping)面坐标問(wen)題。

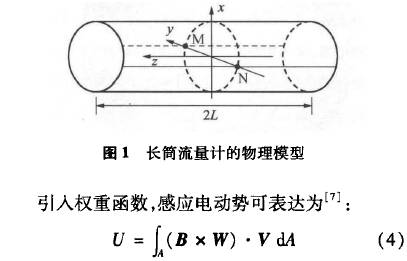
　　式中:A爲(wei)測量管容(rong)積，W爲權重(zhong)函數,W=▽G,G爲格(ge)林函數。W是(shi)三維空間(jian)函數,Wx、Wy、Ws分别(bie)爲W在坐标(biao)軸x、y、z方向，上(shang)分量,對長(zhang)簡流量計(ji)隻考慮y方(fang)向上分量(liang)Wy。假設磁場(chang)方向平行(hang)于x軸,流速(su)平行于z軸(zhou),則B=Bx，V=Vz。由以上(shang)條件,可得(de):
(B×W)·V=BWyV(5)
由式(5)可知(zhi),電極兩端(duan)産生的感(gan)應電動勢(shi)不僅與流(liu)速有關,還(hai)與權重函(han)數分布有(you)關。
3權重函(han)數的仿真(zhen)與分析
3.1單(dan)電極對電(dian)磁流量計(ji)權重函數(shu)數值仿真(zhen)
　　根據格林(lin)函數性質(zhi)和電磁流(liu)量計邊界(jie)條件,可得(de)長筒流量(liang)計權重函(han)數解析式(shi)[7]:

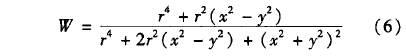
　　式中r爲管(guan)道内半徑(jing)。由式(6)可得(de)管道内電(dian)極所在橫(heng)截面上W的(de)分布情況(kuang),r=1時其等值(zhi)線分布如(ru)圖2所示。
　　由(you)圖2可知,在(zai)管道中心(xin)處W值爲1,沿(yan)着y軸.向電(dian)極M、N處移動(dong)時,W值逐漸(jian)增大;沿着(zhe)x軸向管壁(bi)移動時，W值(zhi)逐漸減小(xiao)至0.5。權重函(han)數越大的(de)區域内的(de)流體速度(du)對電極M、N所(suo)産生感應(ying)電動勢的(de)貢獻越大(da)。由權重函(han)數分布規(gui)律可以看(kan)出,整個測(ce)量區域内(nei)的流體速(su)度對電極(ji)所産生感(gan)應電動勢(shi)的影響程(cheng)度不一樣(yang),這就解釋(shi)了傳統單(dan)電極對電(dian)磁流量計(ji)對流速分(fen)布的敏感(gan)性,導緻其(qi)無法準确(que)測得非軸(zhou)對稱流的(de)平均流速(su)。
　　采用有限(xian)元方法,使(shi)用Malab軟件中(zhong)PDE工具.箱,對(dui)單電極對(dui)電磁流量(liang)計在管道(dao)内電極所(suo)在橫截面(mian)上權重函(han)數分布情(qing)況進行數(shu)值仿真。在(zai)數值仿真(zhen)時,關鍵是(shi)求解格林(lin)函數G,由于(yu)C滿足拉普(pu)拉斯方程(cheng)▽2G=0,假設電磁(ci)流量計邊(bian)界條件如(ru)下:

(4)對求解(jie)區域網格(ge)化，網格劃(hua)分越細,精(jing)度越高,但(dan)計算量會(hui)增大;
(5)求解(jie)橢圓型偏(pian)微分方程(cheng)可得u,即G;
(6)求(qiu)解格林函(han)數G在y方向(xiang)上的梯度(du),即Wy;
(7)畫出Wy的(de)等值線分(fen)布圖。
　　如圖(tu)3所示，爲權(quan)重函數數(shu)值解等值(zhi)線。将其與(yu)圖2進行對(dui)比,發現二(er)者沒有太(tai)大差别。表(biao)明利用有(you)限元方法(fa)計算權重(zhong)函數是高(gao)效可行的(de)方法,并且(qie)可通過增(zeng)加網格密(mi)度來提高(gao)計算精度(du)。

3.2三對電極(ji)電磁流量(liang)計權重函(han)數數值仿(pang)真
　　針對三(san)對電極電(dian)磁流量計(ji),對電極處(chu)于管道橫(heng)截面上不(bu)同位置時(shi)權重函數(shu)的分布情(qing)況分别進(jin)行仿真,結(jie)果如圖4所(suo)示。三對電(dian)極的位置(zhi)分布如下(xia):中間一對(dui)電極橫坐(zuo)标爲x=0,兩側(ce)電極關于(yu)中間電極(ji)對稱,它們(men)到中間電(dian)極的橫向(xiang)距離爲d,d的(de)範圍爲0.1r~0.9r,其(qi)中r爲傳感(gan)器管道内(nei)半徑。
3.3權重(zhong)函數的數(shu)值分析
　　定(ding)義:對管道(dao)橫截面上(shang)權重函數(shu)分布進行(hang)數值仿真(zhen)時,設求解(jie)區域被劃(hua)分成n個網(wang)格,第k個網(wang)格對應的(de)權重函數(shu)值爲Wk(k=1,2,.,n),則權(quan)重函數W的(de)最大偏差(cha)RM可表示爲(wei):RM=MAX

　　應區域内(nei)權重函數(shu)的最大偏(pian)差程度;RD則(ze)反應了區(qu)域内權重(zhong)函數分布(bu)的整體均(jun)勻程度,RD值(zhi)越小，權重(zhong)函數分布(bu)的整體均(jun)勻程度越(yue)理想。
　　依據(ju)上面兩個(ge)指标,計算(suan)電極處于(yu)不同位置(zhi)時權重函(han)數分布均(jun)勻度,如表(biao)1所示。從圖(tu)4和表1可知(zhi),權重函數(shu)分布情況(kuang)不僅與電(dian)極數目有(you)關，還與電(dian)極分布的(de)位置有關(guan);随着兩側(ce)電極與中(zhong)間電極距(ju)離增大,權(quan)重函數的(de)平均值W0逐(zhu)漸減小,即(ji)相同流速(su)對流量計(ji)輸出信号(hao)的貢獻逐(zhu)漸減弱;随(sui)着兩側電(dian)極與中間(jian)電極距離(li)增大,權重(zhong)函數的最(zui)大偏差Rm和(he)RD的值都逐(zhu)漸增大，權(quan)重函數的(de)整體均勻(yun)度逐漸降(jiang)低。


　　權重函(han)數均勻度(du)Rp随電極位(wei)置變化趨(qu)勢如圖5所(suo)示。從表1和(he)圖5可知,對(dui)于三對電(dian)極電磁流(liu)量計,當中(zhong)間一對電(dian)極橫坐标(biao)爲x=0,兩側電(dian)極到中間(jian)電極的橫(heng)向距離d≤0.7r時(shi),整體均勻(yun)度Rp<1.4619,最大偏(pian)差RM<10.6746,即三對(dui)電極電磁(ci)流量計比(bi)傳統單電(dian)極對電磁(ci)流量計權(quan)重函數分(fen)布的更爲(wei)均勻,其管(guan)道橫截面(mian).上不同位(wei)置流體速(su)度對流量(liang)計輸出信(xin)号的貢獻(xian)更趨向-緻(zhi),表明三對(dui)電極電磁(ci)流量計對(dui)流速分布(bu)的敏感性(xing)減弱;權重(zhong)函數平均(jun)值W0>0.0851,表明相(xiang)比單電極(ji)對電磁流(liu)量計,管道(dao)橫截面上(shang)相同流速(su)對流量計(ji)輸出信号(hao)的貢獻增(zeng)強,即在相(xiang)同條件下(xia),三對電極(ji)電磁流量(liang)計可獲得(de)更強的感(gan)應電動勢(shi)信号。

　　以上(shang)針對三對(dui)電極電磁(ci)流量計權(quan)重函數分(fen)布随電極(ji)位置變化(hua)情況進行(hang)了仿真分(fen)析，結果爲(wei)多電極電(dian)磁流量計(ji)的結構優(you)化提供了(le)參考依據(ju),具有-定的(de)理論指導(dao)意義。雖然(ran)從理論上(shang)電極數目(mu)越多,流體(ti)平均速度(du)的測量精(jing)度越高,但(dan)從實際制(zhi)作、成本和(he)可靠性來(lai)講,電極數(shu)目不可能(neng)無限增多(duo),而且電極(ji)數目的增(zeng)加會延長(zhang)數據采集(ji)時間,導緻(zhi)系統實時(shi)性降低,通(tong)常隻要測(ce)量精度達(da)到要求就(jiu)可以了。當(dang)然對精度(du)有特殊要(yao)求時,可相(xiang)應增加或(huo)減少電極(ji)數目。
4結論(lun)　
　　 采用有限(xian)元方法對(dui)傳統單電(dian)極對電磁(ci)流量計權(quan)重函數分(fen)布進行了(le)數值仿真(zhen),将仿真結(jie)果與已有(you)權重函數(shu)解析解作(zuo)對比分析(xi),驗證了有(you)限元方法(fa)求解權重(zhong)函數的可(ke)行性和有(you)效性;針對(dui)三對電極(ji)電磁流量(liang)計,電極在(zai)不同位置(zhi)時,對電極(ji)所在橫截(jie)面上權重(zhong)函數分布(bu)情況分别(bie)進行數值(zhi)仿真;定義(yi)了兩個描(miao)述權重函(han)數分布均(jun)勻度的指(zhi)标:最大偏(pian)差和整體(ti)均勻度。依(yi)據這兩個(ge)指标，在電(dian)極數目和(he)位置不同(tong)情況下，分(fen)别對權重(zhong)函數進行(hang)仿真分析(xi)。結果表明(ming)通過合理(li)設計電極(ji)位置,三電(dian)極對電磁(ci)流量計在(zai)權重函數(shu)分布均勻(yun)度和平均(jun)強度兩方(fang)面都優于(yu)單電極對(dui)電磁流量(liang)計。

以上内(nei)容源于網(wang)絡，如有侵(qin)權聯系即(ji)删除!