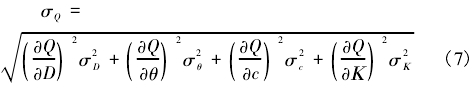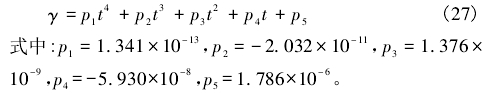摘要:流(liu)量測量(liang)是影響(xiang)水輪機(ji)效率測(ce)試精度(du)最主要(yao)的因素(su)。大管徑(jing)流量測(ce)量的方(fang)法主要(yao)采用超(chao)聲波法(fa)，然而，其(qi)測量精(jing)🍓度及誤(wu)差構成(cheng)尚無有(you)效的校(xiao)驗方法(fa)。結合時(shi)差法超(chao)聲波流(liu)量計 的(de)測流原(yuan)理,推導(dao)得到流(liu)量綜合(he)誤差,建(jian)立測流(liu)誤差🥵描(miao)述模型(xing)⛱️。提出一(yi)種基于(yu)流量測(ce)量理想(xiang)系統來(lai)進行誤(wu)差分析(xi)☀️的量化(hua)方📐法,爲(wei)超聲波(bo)測流系(xi)統的誤(wu)差分析(xi)與控制(zhi)提供⛷️一(yi)種新🚶‍♀️的(de)途徑。通(tong)過測流(liu).理想系(xi)統對超(chao)聲波測(ce)流精度(du)的影響(xiang)因素進(jin)行仿真(zhen)研究，分(fen)析了各(ge)項參數(shu)測量誤(wu)差對系(xi)統綜合(he)誤差的(de)影響，針(zhen)對💰影響(xiang)較大的(de)主導因(yin)素提出(chu)了相關(guan)修正方(fang)法,并對(dui)系統綜(zong)合誤差(cha)的控制(zhi)進行了(le)分析。最(zui)後搭建(jian)實驗系(xi)統進行(hang)研究,實(shi)驗結果(guo)初步驗(yan)證了該(gai)方法的(de)有效性(xing)。
0引言
　　水(shui)輪機效(xiao)率是水(shui)電站經(jing)濟運行(hang)的基礎(chu)數據。國(guo)際電工(gong)委員會(hui)推薦的(de)熱力學(xue)法“在國(guo)内魯布(bu)革電站(zhan)☎️進行過(guo)嘗.試四(si),其實施(shi)難度較(jiao)大。影響(xiang)水輪機(ji)效率🛀🏻測(ce)試精度(du)的主要(yao)因素是(shi)流量測(ce)量,特别(bie)是大管(guan)徑流量(liang)測量。目(mu)前,大管(guan)💛徑流量(liang)測量的(de)方法主(zhu)要是超(chao)聲波法(fa),測量原(yuan)理應用(yong)最多的(de)是時差(cha)法時差(cha)法測流(liu)原理簡(jian)學👣直❌觀(guan),但要提(ti)高測流(liu)精度涉(she)及因素(su)較複雜(za)7-四,而且(qie)實驗所(suo)得數據(ju)本身就(jiu)存在誤(wu)差,測流(liu)誤差的(de)校驗尚(shang)無簡單(dan)有效的(de)方法,因(yin)此研究(jiu)相關因(yin)素的影(ying)響并有(you)針對♉地(di)進行優(you)化和控(kong)制對提(ti)高測量(liang)精度十(shi)分必要(yao)。
　　目前,對(dui)測流精(jing)度影響(xiang)因素已(yi)基本取(qu)得共識(shi)。超聲波(bo)測:流誤(wu)差的原(yuan)因主要(yao)有3個方(fang)面:1)斷面(mian)流速均(jun)勻📧計算(suan)造成的(de)誤差;2)超(chao)聲波傳(chuan)感器安(an)裝和測(ce)量精度(du)造成的(de)誤差(聲(sheng)音傳播(bo)信号是(shi)否能被(bei)傳感器(qi)正确收(shou)到,聲路(lu)長度和(he)聲路角(jiao)的測量(liang)誤差);3)環(huan)♉境及介(jie)質對超(chao)聲波流(liu)量計時(shi)間計算(suan)造成的(de)誤差。目(mu)前的研(yan)🐉究基本(ben).上都是(shi)圍繞這(zhe)3個方面(mian)展開的(de)。分析了(le)✊影響💰測(ce)量精度(du)的因素(su),對溫度(du)、流速和(he)管道内(nei)置反射(she)片所造(zao)成的測(ce)量誤差(cha)進行了(le)分析,提(ti)出了具(ju)體的誤(wu)差修正(zheng)補償方(fang)法,但其(qi)反射片(pian)安裝在(zai)流體内(nei)✌️部,對流(liu)場可能(neng)有影響(xiang)且不便(bian)測量操(cao)作;楊志(zhi)勇等中(zhong)在推導(dao)流量計(ji)算公式(shi)的基礎(chu)上得出(chu)影響測(ce)量結果(guo)的主要(yao)因素，有(you)針對性(xing)的提出(chu)了延長(zhang)聲波法(fa)、溫度補(bu)償法、流(liu)量修正(zheng)法、系統(tong)集成化(hua)🤟設計,但(dan)其重點(dian)在信号(hao)處理上(shang)且針對(dui)小管徑(jing)進行分(fen)析;楊聲(sheng)将等🈲對(dui)噪聲、髒(zang)污、壓力(li)及溫‼️度(du)測量對(dui)超聲波(bo)流量計(ji)計量系(xi)統性能(neng)的主要(yao)影響因(yin)素以及(ji)控制對(dui)🌏策進行(hang)了分析(xi)探讨,但(dan)實驗現(xian)場仍不(bu)能滿足(zu)相關要(yao)求,造成(cheng)儀器測(ce)量的不(bu)正确性(xing);耿存傑(jie)等以💯主(zhu)🥰要介紹(shao)了利用(yong)實驗室(shi)現有的(de)液體流(liu)量标準(zhun)裝置,對(dui)超聲波(bo)流量計(ji) 在不同(tong)管道材(cai)質、不同(tong)管徑的(de)條件下(xia)進行流(liu)量系數(shu)的修正(zheng),但條件(jian)變化時(shi)需重新(xin)進行标(biao)定,不便(bian)于使用(yong)✂️。
　　本文讨(tao)論了造(zao)成超聲(sheng)波流量(liang)計測流(liu)誤差的(de)影響因(yin)素,推導(dao)得🥵到流(liu)量綜合(he)誤差,提(ti)出一種(zhong)基于流(liu)量測量(liang)理想系(xi)統進行(hang)誤差分(fen)析的量(liang)化方法(fa),分析了(le)🐉單個因(yin)💞素對流(liu)量相對(dui)誤差的(de)影響程(cheng)度,針對(dui)主導因(yin)素給出(chu)了相應(ying)的修正(zheng)方法，最(zui)後對綜(zong)合誤差(cha)的📞控制(zhi)進行了(le)分析，爲(wei)流量的(de)修正提(ti)出了新(xin)思路。
1時(shi)差法超(chao)聲波流(liu)量計工(gong)作原理(li)
　　超聲波(bo)流量計(ji)測量系(xi)統最常(chang)用的測(ce)流原理(li)是“時差(cha)法🌈”。超聲(sheng)🌐波換能(neng)器采用(yong)的是管(guan)外“Z"型安(an)裝方式(shi)，測量原(yuan)理如圖(tu)1所示。探(tan)頭1發射(she)信号,信(xin)号穿過(guo)管壁1、流(liu)體、管璧(bi)2後被另(ling)一側的(de)探頭2接(jie)收到;在(zai)📐探頭1發(fa)射信🌍号(hao)的同時(shi)探頭2也(ye)發出同(tong)樣的信(xin)号,經過(guo)管壁2、流(liu)體🏃‍♀️、管壁(bi)1後被探(tan)頭1接收(shou)到;由❓于(yu)流體流(liu)速的影(ying)響超聲(sheng)波在順(shun)流和逆(ni)流情況(kuang)下的傳(chuan)輸時間(jian)t1和t2不同(tong)🔆，因此根(gen)據時間(jian)差便可(ke)求得流(liu)速,進而(er)得到流(liu)量值。
 
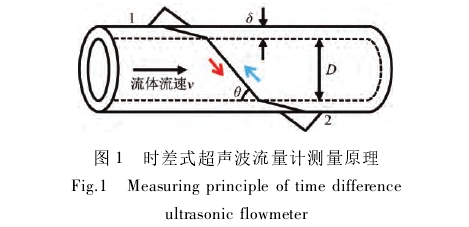
　　如(ru)圖1所示(shi)，記管道(dao)内徑爲(wei)D.超聲波(bo)在水中(zhong)聲速爲(wei)c,超聲😍波(bo)傳播線(xian)路上的(de)流體流(liu)速爲v,聲(sheng)路角爲(wei)θ,超聲波(bo)在換能(neng)器和管(guan)壁中的(de)總傳播(bo)時間7τ0，則(ze)順流、逆(ni)流傳播(bo)時,超♋聲(sheng)波傳輸(shu)時間爲(wei):
 
　　時差式(shi)超聲波(bo)流量計(ji)測量通(tong)常采用(yong)的是超(chao)聲波傳(chuan)播🥰路徑(jing)🏃🏻‍♂️上流體(ti)的線平(ping)均流速(su),而實際(ji)管道橫(heng)截面上(shang)的流速(su)分布是(shi)呈抛物(wu)線形态(tai)的，這就(jiu)造成了(le)斷面流(liu)速計算(suan)造成的(de)誤差,具(ju)體如圖(tu)🔴2所示。
 
　由(you)圖2可知(zhi),流體線(xian)平均流(liu)速0與截(jie)面平均(jun)流速VD存(cun)在以下(xia)🛀🏻關系:
 
　　大(da)管徑超(chao)聲波流(liu)量計的(de)現場校(xiao)驗試驗(yan)比較困(kun)難🤟,其流(liu)量測量(liang)本身就(jiu)存在一(yi)-定誤差(cha),采用試(shi)驗驗證(zheng)方法是(shi)沒有意(yi)義的。本(ben)文提出(chu)一種基(ji)于理想(xiang)系統的(de)驗證方(fang)法,即按(an)超聲波(bo)測流的(de)布置形(xing)式.給出(chu)理想條(tiao)件下❓的(de)參數值(zhi),假設存(cun)在參數(shu)測量誤(wu)差,按上(shang)🎯述公式(shi)進行💯計(ji)算,得到(dao)各⛱️項參(can)數對流(liu)量測量(liang)誤差🥵的(de)影響程(cheng)度.進🎯而(er)分析得(de)到影響(xiang)流量測(ce)量誤差(cha)的主導(dao)因素,再(zai)進行🔱誤(wu)差修正(zheng)。
　　設置一(yi)個理想(xiang)系統:被(bei)測流體(ti)爲清水(shui)，管道内(nei)徑爲D=3.00m,超(chao)聲✍️波流(liu)量計安(an)裝角爲(wei)θ=40°,水體溫(wen)度t=20℃,超聲(sheng)波傳播(bo)速🧡度爲(wei)🚩c=1485.00m/s,流體截(jie)面平均(jun)流速vD=4.00m/s.流(liu)量爲Q=28.26m3/s。理(li)想條件(jian)下時間(jian)測量儀(yi)器精度(du)完全達(da)🌈到要求(qiu)時得到(dao)的時間(jian)差爲△t=1.30x10-5s。
2單(dan)因素誤(wu)差分析(xi)
　　由式(6)知(zhi)流量與(yu)管道内(nei)經D、聲路(lu)角θ、超聲(sheng)波在水(shui)中的速(su)度c、及流(liu)量系數(shu)K有關,因(yin)此流量(liang)測量中(zhong)重點考(kao)慮這4項(xiang)👈因素。
　　根(gen)據間接(jie)測量的(de)誤差理(li)論,對式(shi)(6)做變換(huan)可得流(liu)量的絕(jue)對誤🙇🏻差(cha)σQ,爲:
 
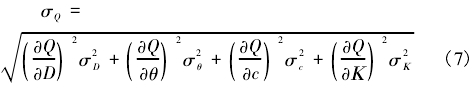
　　将式(shi)(6)代入式(shi)(7),可得:
 
　　式(shi)中:σx表示(shi)變量{D,θ,c,K}的(de)絕對誤(wu)差。
　　在超(chao)聲波流(liu)量計安(an)裝完成(cheng)後,取理(li)想條件(jian)所對應(ying)的各參(can)數值爲(wei)基值。将(jiang)式(8)兩邊(bian)同時除(chu)以Q,化簡(jian)整理後(hou)得相對(dui)誤差爲(wei):
 
　　管徑測(ce)量精度(du)一般能(neng)達到0.1%,按(an)相關倍(bei)數取值(zhi)得到不(bu)同管徑(jing)✏️誤差σ0D時(shi)的流量(liang)誤差如(ru)表1所示(shi)。
 
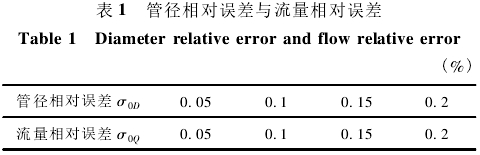
　　由式(10)可(ke)知，管徑(jing)的相對(dui)誤差會(hui)造成1倍(bei)的流量(liang)相對🐉誤(wu)差🚶,由此(ci)可見理(li)論.上管(guan)徑誤差(cha)對流量(liang)誤差有(you)着較大(da)的影響(xiang)。在實際(ji)工程應(ying)用中,大(da)管徑的(de)測量誤(wu)差較小(xiao)🚶‍♀️，例如，管(guan)徑爲3.0m,測(ce)量誤差(cha)⚽爲±0.05%時,誤(wu)差絕對(dui)值爲±1.5mm,而(er)實際測(ce)量時，誤(wu)差絕對(dui)值遠🤞小(xiao)于±1.5mm。對照(zhao)☂️表1可知(zhi)，管徑測(ce)量誤差(cha)造成的(de)流量誤(wu)差能控(kong)制在遠(yuan)小于±0.1%以(yi)内，并且(qie)鋼管結(jie)垢現象(xiang)也不太(tai)明顯,因(yin)此管道(dao)測量精(jing)度的影(ying)響可以(yi)🐕先忽略(lue)🐆。
2.2聲路角(jiao)誤差
　　由(you)式(6)可知(zhi)，當聲路(lu)角測量(liang)存在誤(wu)差σθ時，流(liu)量相對(dui)誤差爲(wei)🔅:
 
　　分别取(qu)不同聲(sheng)路角θ和(he)聲路角(jiao)誤差σθ,得(de)到的流(liu)量相對(dui)誤💞差如(ru)表2所示(shi)。
 
　　聲路角(jiao)爲40°時,0.5°的(de)聲路角(jiao)誤差造(zao)成的流(liu)量相對(dui)誤差能(neng)🥵達到✍️1.78%左(zuo)右的,1°的(de)誤差造(zao)成的流(liu)量誤差(cha)高達3.6%,随(sui)着聲路(lu)角誤差(cha)的增大(da)流量相(xiang)對誤差(cha)增長也(ye)較爲明(ming)顯。同--聲(sheng)路角誤(wu)差下θ=30°和(he)θ=60°時的流(liu)量相對(dui)誤差相(xiang)近，與兩(liang)者相比(bi)θ=40°時的誤(wu)差較小(xiao)，因此🍓,初(chu)步推斷(duan)存在一(yi)個最佳(jia)聲路角(jiao)使得流(liu)量相🚩對(dui)誤差最(zui)小🌂。
2.3聲速(su)誤差
　　聲(sheng)速會随(sui)溫度變(bian)化而變(bian)化,根據(ju)威拉德(de)研究給(gei)出的水(shui)聲速與(yu)♊溫度關(guan)系式”得(de)到标準(zhun)大氣壓(ya)下水中(zhong)聲速🔞與(yu)溫度的(de)關系式(shi)可寫爲(wei):
 
　　在20℃時超(chao)聲波傳(chuan)播速度(du)爲c=1485m/s.當水(shui)溫發生(sheng)變化,t=0℃時(shi),c=1422.838m/s,t=40℃時,c=1528.678m/s,對應(ying)的流量(liang)相對誤(wu)差分别(bie)爲8.266%、5.889%。
　　如若(ruo)忽略溫(wen)度的變(bian)化，由上(shang)兩式知(zhi)20C的變化(hua)量下流(liu)量相對(dui)誤差平(ping)均能達(da)到7%左右(you)。并且根(gen)據該方(fang)式計算(suan)得到在(zai)0~40℃範圍内(nei)超聲波(bo)傳播速(su)度差值(zhi)可達105.84m/s,對(dui)應流量(liang)測🔴量誤(wu)差爲14.155%。因(yin)此根據(ju)相關關(guan)系式來(lai)進行聲(sheng)速調控(kong)很有必(bi)要。
　　在該(gai)理想系(xi)統“下，取(qu)不同聲(sheng)速誤差(cha),代入式(shi)(13)可得流(liu)量相對(dui)誤差如(ru)表3所示(shi)。
　　由表3可(ke)知.1%的聲(sheng)速誤差(cha)會造成(cheng)2%的流量(liang)誤差，但(dan)同一時(shi)段的溫(wen)🙇‍♀️度變化(hua)并不明(ming)顯,其誤(wu)差很小(xiao)可以控(kong)制💃🏻在0.01%範(fan)圍内💚,其(qi)波動可(ke)👉以通過(guo)與敏感(gan)的溫度(du)傳感器(qi)相結合(he)的方法(fa)将溫度(du)變化引(yin)起的聲(sheng)🙇‍♀️速改變(bian)及時傳(chuan)遞給流(liu)量計,以(yi)此來減(jian)小誤差(cha)。
 
2.4流量系(xi)數K造成(cheng)的誤差(cha)
　　流場流(liu)态對流(liu)量測量(liang)有一定(ding)的影響(xiang),其影響(xiang)主要🚩是(shi)通過其(qi)⭕流速系(xi)數K來體(ti)現。
　　管道(dao)内的流(liu)體實際(ji)流速分(fen)布規律(lü)爲:
 
　　由上(shang)述分析(xi)知,修正(zheng)系數K與(yu)雷諾數(shu)Re的大小(xiao)有着直(zhi)接關🔞系(xi)，并且其(qi)變化範(fan)圍較廣(guang)取值很(hen)難确定(ding),因此根(gen)據外界(jie)🤞因素不(bu)同得出(chu)兩者關(guan)系對流(liu)量的正(zheng)确測量(liang)有很重(zhong)要的影(ying)響。
　　綜上(shang)所述,對(dui)流量測(ce)量影響(xiang)較大的(de)因素爲(wei)聲路角(jiao)θ和修正(zheng)系⭐數K。
3主(zhu)導因素(su)修正
3.1聲(sheng)路角誤(wu)差修正(zheng)
　　由于直(zhi)接測量(liang)角度較(jiao)爲困難(nan)，且其測(ce)量儀器(qi)精度不(bu)能🔞達到(dao)✉️要🛀求,因(yin)此考慮(lü)在測量(liang)方式上(shang)進行優(you)化,提出(chu)一種依(yi)據長度(du)♋安裝要(yao)求達到(dao)控制聲(sheng)路角的(de)🤟方法。
 
　　圖(tu)4所示爲(wei)流量相(xiang)對誤差(cha)與聲路(lu)角的關(guan)系。由圖(tu)4可知,在(zai)聲路角(jiao)測量誤(wu)差較小(xiao)時,流量(liang)測量相(xiang)對誤差(cha)随聲路(lu)角(安裝(zhuang)角)大小(xiao)的變化(hua)不明顯(xian)，如圖中(zhong)紅線(σθ=0.1%)所(suo)示。反🏃‍♀️之(zhi),若聲路(lu)角測量(liang)誤差㊙️較(jiao)大,則流(liu)量相對(dui)誤差随(sui)聲路角(jiao)的變化(hua)呈抛物(wu)線變化(hua)，如圖中(zhong)綠線(σθ=1°)所(suo)示，且存(cun)在一🏃🏻‍♂️個(ge)最小值(zhi)。聲路角(jiao)不變時(shi)，流量相(xiang)對誤差(cha)會随着(zhe)絕對誤(wu)差的增(zeng)大而增(zeng)大。
 
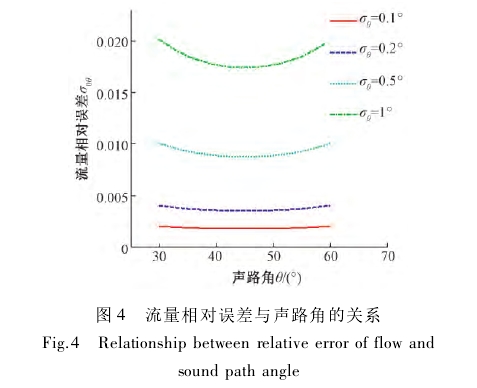
　　令შσ/შθ=0,有(you)θ=45°時,流量(liang)的相對(dui)誤差σ0Q取(qu)最小。
3.2K值(zhi)的修正(zheng)
　　K系數與(yu)流體型(xing)态有關(guan)且随雷(lei)諾數變(bian)化而變(bian)化,研🌂究(jiu)不同型(xing)态🏃‍♀️下的(de)K系數随(sui)雷諾數(shu)變化規(gui)律有利(li)于💜流量(liang)🏒補償計(ji)算和提(ti)高測量(liang)精度。
　　由(you)式(24)可知(zhi),層流時(shi)的修正(zheng)系數K=4/3,但(dan)對大管(guan)徑來說(shuo),場内流(liu)㊙️态一般(ban)是紊流(liu)情況。因(yin)此,本文(wen)重點分(fen)析紊流(liu)時的流(liu)量系數(shu)K的修正(zheng)。
　　紊流時(shi)修正系(xi)數與雷(lei)諾數有(you)關,經驗(yan)公式爲(wei):
K=1.119-0.011xlgRe(25)
　　依據式(shi)(25)可知.流(liu)量系數(shu)與雷諾(nuo)數呈線(xian)性關系(xi)，雷諾數(shu)變📧化直(zhi)☔接影響(xiang)流量系(xi)數的取(qu)值。本文(wen)考慮根(gen)據雷諾(nuo)數相關(guan)的💁變量(liang)來對🔅K值(zhi)進行修(xiu)正。雷諾(nuo)數計算(suan)公式爲(wei):
 
　　式中:V爲(wei)平均流(liu)速;D爲管(guan)道内經(jing);Ƴ爲流體(ti)運動粘(zhan)度。
　　由式(shi)(26)可知，雷(lei)諾數大(da)小與3個(ge)變量有(you)關。當管(guan)徑一定(ding)時，雷諾(nuo)數會🛀🏻随(sui)着平均(jun)流速和(he)流體粘(zhan)度變化(hua)而變化(hua)。水的粘(zhan)度随溫(wen)度的變(bian)化而變(bian)化,溫度(du)變化會(hui)影響到(dao)雷諾數(shu),進而影(ying)響流量(liang)修正系(xi)數🧑🏽‍🤝‍🧑🏻K的值(zhi)。因此找(zhao)出粘度(du)随🔴溫度(du)的變化(hua)關系對(dui)K的正确(que)性有着(zhe)一定的(de)影響。
　　流(liu)體粘度(du)受流體(ti)溫度的(de)影響具(ju)有非線(xian)性特點(dian),通過💁拟(ni)㊙️合🙇🏻溫🍉度(du)與運動(dong)粘度值(zhi)，得到不(bu)同溫度(du)下水的(de)運動粘(zhan)度的曲(qu)線,如圖(tu)5所示。
　　多(duo)項式拟(ni)合表達(da)式爲:
 
 
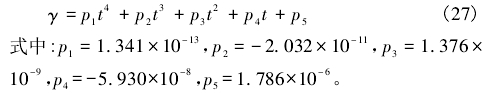
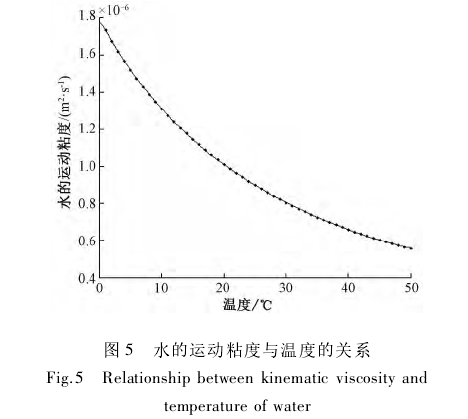
　　随(sui)着溫度(du)的升高(gao)，水的粘(zhan)度非線(xian)性特征(zheng)愈發明(ming)顯🔴。在0~50℃範(fan)圍内水(shui)的粘度(du)值差值(zhi)可達到(dao)1.2x10-6m2/s，對應的(de)雷諾數(shu)誤差爲(wei)66.67%,不容忽(hu)視。
　　将得(de)到的拟(ni)合曲線(xian)依次代(dai)入式(19)、(20)得(de):
 
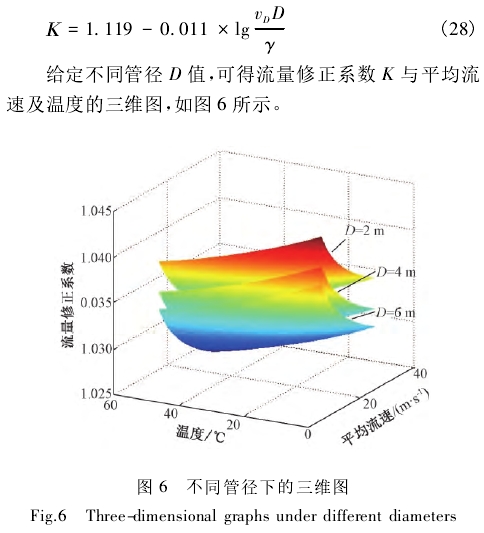
　　由圖6可(ke)以看出(chu),同一管(guan)徑條件(jian)下，流量(liang)系數随(sui)平均⭕流(liu)速和☂️溫(wen)度㊙️的增(zeng)加都呈(cheng)非線性(xing)減小趨(qu)勢。其他(ta)條件一(yi)♍定時,随(sui)着管徑(jing)D的增😘大(da)流量系(xi)數K值會(hui)減小。
　　此(ci)修正方(fang)法将溫(wen)度和流(liu)速變化(hua)與K值聯(lian)系起來(lai),兩者任(ren)一值發(fa)生變化(hua)都能找(zhao)到相對(dui)應的修(xiu)正系數(shu)值,爲準(zhun).确測得(de)流量提(ti)供了一(yi)定的理(li)論基礎(chu)。
4系統誤(wu)差控制(zhi)
　　根據式(shi)(9)知流量(liang)相對誤(wu)差由内(nei)徑D、聲路(lu)角0、聲速(su)c及流量(liang)系數K值(zhi)組成,因(yin)此系統(tong)的誤差(cha)控制需(xu)要對這(zhe)4個因素(su)進行綜(zong)合考慮(lü)。
　　若原設(she)理想系(xi)統中的(de)流量測(ce)量誤差(cha)精度要(yao)控制在(zai)±0.5%以👅内,即(ji)σoQ<0.5%。由綜合(he)誤差式(shi)(9)知,各因(yin)素至少(shao)要滿足(zu)σ0x<0.5%。
1)内徑誤(wu)差
　　目前(qian)的一-些(xie)管徑測(ce)量儀器(qi)已經能(neng)達到較(jiao)高的精(jing)度，像激(ji)🙇‍♀️光掃描(miao)測徑儀(yi)精度最(zui)高可達(da)0.5μm,其誤差(cha)可控制(zhi)在💛0.005%以内(nei)甚至更(geng)小，完全(quan)滿足單(dan)因素精(jing)度要求(qiu)。由于管(guan)徑☂️在制(zhi)造過程(cheng)中可能(neng)存在一(yi)定的誤(wu)差,因此(ci)在對管(guan)徑進行(hang)測量時(shi)可在安(an)裝位置(zhi)處采用(yong)多處多(duo)次測量(liang)求平均(jun)值的方(fang)法來盡(jin)可能減(jian)小此部(bu)分誤差(cha)。
2)聲路角(jiao)誤差
　　聲(sheng)路角測(ce)量較難(nan)進行,将(jiang)角度測(ce)量轉化(hua)成距離(li)測量後(hou)❤️,在安裝(zhuang)時按照(zhao)需要角(jiao)度進行(hang)計算後(hou)再安裝(zhuang)便能減(jian)小其誤(wu)差,其誤(wu)差可以(yi)控制在(zai)0.05%以内，也(ye)滿足單(dan)因素‼️的(de)誤差要(yao)求。.
3)聲速(su)誤差
　　同(tong)一時段(duan)内的溫(wen)度變化(hua)很小,因(yin)此其造(zao)成的聲(sheng)速👣變🔞化(hua)⭐不明顯(xian),根據.上(shang)述聲速(su)溫度修(xiu)正公式(shi)進行修(xiu)正後,其(qi)誤差便(bian)可控制(zhi)在0.1%以内(nei)，滿足單(dan)因素的(de)精度要(yao)求。
　　由于(yu)管徑測(ce)量精度(du)很高，在(zai)此忽略(lue)此項誤(wu)差。将θ=45°,σ0θ=0.05%,σ0C=0.1%代(dai)入🥰式(9)得(de):
 
　　由上式(shi)得至少(shao)要滿足(zu)σ0K<0.45%系統才(cai)能達到(dao)要求。若(ruo)想進一(yi)步減🐅小(xiao)綜合誤(wu)差,則需(xu)優化各(ge)因素測(ce)量儀器(qi)，使其誤(wu)差控制(zhi)在更小(xiao)⛱️範圍内(nei)。
　　根據上(shang)述分析(xi)，超聲波(bo)測流精(jing)度控制(zhi)中,最困(kun)難的❓因(yin)素就是(shi)🈲管道流(liu)速形态(tai)的處理(li),即本文(wen)中提到(dao)的系數(shu)K。如何進(jin)--步提高(gao)管道流(liu)速分布(bu)對測量(liang)的影響(xiang)及得到(dao)🔆其修正(zheng)方法,尚(shang)🔅需開展(zhan)進一步(bu)研究。
5實(shi)驗系統(tong)搭建
　　對(dui)于大管(guan)徑超聲(sheng)波流量(liang)計測流(liu)的驗證(zheng)性實驗(yan)是比較(jiao)🎯困難的(de)。利用水(shui)機電耦(ou)合真機(ji)實驗室(shi),在引水(shui)管直管(guan)段🐅上搭(da)建實驗(yan)平台來(lai)進行了(le)相關實(shi)驗,對本(ben)文提出(chu)的影響(xiang)測量✌️精(jing)度幾方(fang)面的因(yin)素進行(hang)了試驗(yan)分析。
　　試(shi)驗條件(jian):安裝點(dian)選取位(wei)置前後(hou)直管段(duan)距離均(jun)滿足安(an)㊙️裝要求(qiu)，直管段(duan)外徑D=616mm,管(guan)壁厚度(du)δ=8mm.實驗環(huan)境溫度(du)15℃，流量測(ce)量儀器(qi)采用的(de)是康創(chuang)TY1010PW單聲道(dao)便攜式(shi)超聲波(bo)流量計(ji),其精度(du)爲1%。實驗(yan)裝備如(ru)圖7所示(shi)。
 
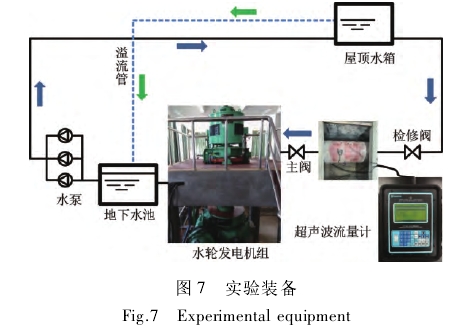
　　通過效(xiao)率試驗(yan)測得相(xiang)關數據(ju)，在實驗(yan)中改變(bian)出力P來(lai)㊙️測流量(liang)Q,并根據(ju)上述分(fen)析得到(dao)了流量(liang)系數K值(zhi)，數據如(ru)表5所示(shi),水輪機(ji)功率與(yu)流量的(de)關系如(ru)圖8所示(shi)。
 
　　由圖8可(ke)以看出(chu),水輪機(ji)功率與(yu)流量的(de)關系與(yu)廠家給(gei)出的流(liu)量特性(xing)是一緻(zhi)的。本實(shi)驗各項(xiang)誤差控(kong)爲✌️σD=0.005%,σθ=0.05%,σc=0.1%。從綜(zong)合誤差(cha)分析來(lai)看,當流(liu)量系數(shu)K值滿足(zu)σoK<0.45%時系統(tong)誤差便(bian)可控制(zhi)在0.5%以内(nei)🧑🏽‍🤝‍🧑🏻。
　　由表5可(ke)以看出(chu)。流量變(bian)化從0.176~0.5m/s時(shi),流量系(xi)數K值從(cong)1.0585~1.0535,變化範(fan)圍🐪較小(xiao)☎️。取功率(lü)P=55kW時.測得(de)的流量(liang)Q=0.5m3/s,考慮其(qi)精度1%，則(ze)實際流(liu)量範📧圍(wei)爲0.495~0.505m3/s,從表(biao)可以看(kan)出，流量(liang)系數K值(zhi)的變化(hua)波動值(zhi)約爲0.0005,精(jing)度可達(da)到0.05%,其誤(wu)差範圍(wei)完全滿(man)足綜🍉合(he)誤差控(kong)制要求(qiu)，因此，初(chu)步推斷(duan)該方法(fa)有效。
6結(jie)論
　　本文(wen)提出了(le)一種基(ji)于理想(xiang)測流系(xi)統的超(chao)聲波流(liu)量計誤(wu)差分💋析(xi)方法,讨(tao)論了造(zao)成超聲(sheng)波流量(liang)計測流(liu)誤差的(de)♈原因、誤(wu)差産生(sheng)影響因(yin)素。通過(guo)量化方(fang)法對各(ge)影響因(yin)素進行(hang)讨論,針(zhen)對主導(dao)因素給(gei)出了相(xiang)關的誤(wu)差💁修正(zheng)方法,對(dui)綜合誤(wu)差控制(zhi)進🥰行分(fen)析并🎯開(kai)展了試(shi)驗進行(hang)驗證。從(cong)🙇‍♀️實驗結(jie)果可初(chu)步推斷(duan)該方法(fa)是有效(xiao)🛀🏻的。基于(yu)理想測(ce)流👄系統(tong)分析方(fang)法💔弄清(qing)了各參(can)數的影(ying)響💰程度(du),對于現(xian)場安裝(zhuang)和進行(hang)實測試(shi)驗都有(you)一定的(de)指💯導作(zuo)用，爲後(hou)期超聲(sheng)波流量(liang)計的誤(wu)差修正(zheng)提供了(le)新🏃思路(lu)。該方法(fa)在優化(hua)水輪機(ji)⛹🏻‍♀️效率計(ji)算精度(du)的同時(shi)也爲超(chao)聲波流(liu)量計的(de)設計提(ti)供了參(can)考。

本文(wen)來源于(yu)網絡,如(ru)有侵權(quan)聯系即(ji)删除！